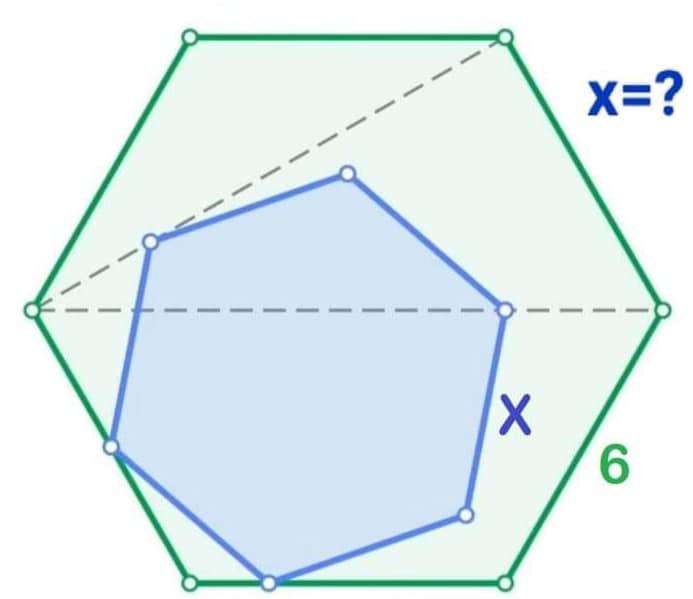
Mathematics Question and Solution
Calculating x, side length of the inscribed regular hexagon.
a = 2x units.
a is twice the side length of the inscribed regular hexagon.
b = ⅙*180(6-2)
b = 120°
b is the single interior angle of the regular hexagon.
c = ½(6)
c = 3 units.
It implies;
d² = 6²+3²-2*3*6cos120
d = 7.9372539332 units.
d = 3√(7) units.
Notice.
d = 2x
2x = 3√(7)
x = ½*3√(7)
x = 1.5√(7) units.
x = 3.9686269666 units.