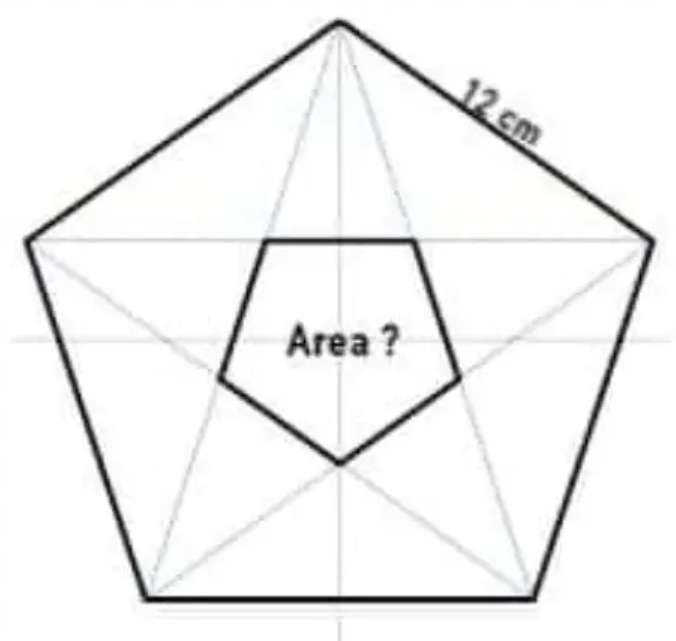
Mathematics Question and Solution
Calculating the area of the inscribed regular pentagon.
Let the single side length of the inscribed regular pentagon be x.
12²=2y²-2y²cos108
y = √(144/(2-2cos108))
y = 7.416407865 cm.
Therefore;
x = √(2(7.416407865)²-2(7.416407865)²cos36)
x = 4.58359213501 cm.
Therefore area inscribed regular pentagon is;
(5*4.58359213501²)/(4tan(36))
= 36.1460548598 cm².