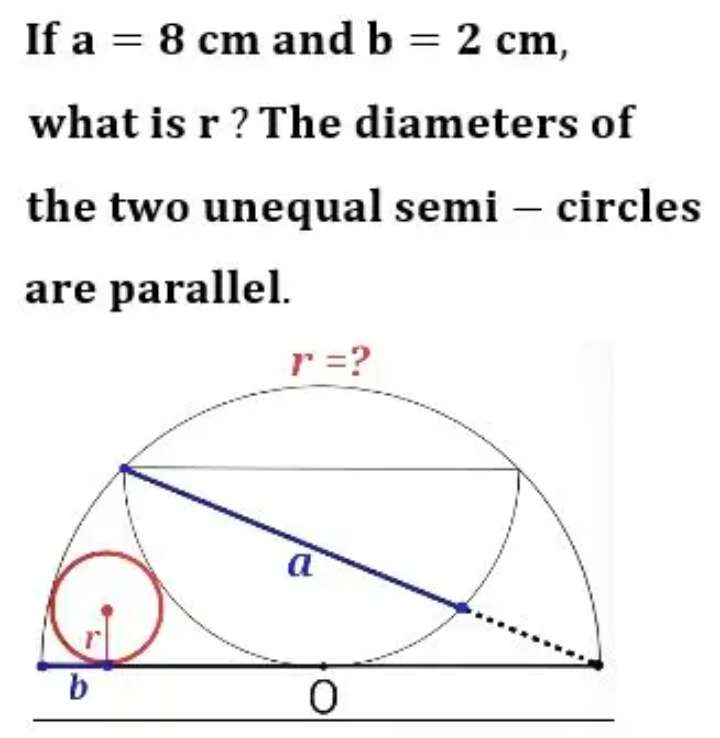
Mathematics Question and Solution
Let c be the radius of the ascribed half circle.
d² = 2c²
d = √(2)c cm.
d is the diameter of the inscribed half circle.
e = ½(d)
e = ½(√(2)c) cm.
e is the radius of the inscribed half circle.
Notice.
a = 8 cm.
8² = f²+(√(2)c)²
f = √(64-2c²) cm.
g = 8+f
g = (8+√(64-2c²)) cm.
h = c+e
h = (c+½(√(2)c)) cm.
Calculating c.
(8+√(64-2c²))² = (c+½(√(2)c))²+(½(√(2)c))²
64+16√(64-2c²)+64-2c² = c²+√(2)c²+½(c²)+½(c²)
128+16√(64-2c²) = 4c²+√(2)c²
128+16√(64-2c²) = 5.4142135624c²
16√(64-2c²) = 5.4142135624c²-128
16²(64-2c²) = (5.4142135624c²-128)²
16384-512c² = 29.3137084993c⁴-1386.0386719744c²+16384
29.3137084993c⁴-874.0386719744c² = 0
29.3137084993c⁴ = 874.0386719744c²
29.3137084993c² = 874.0386719744
c² = 29.8167211424
c = √(29.8167211424)
c = 5.4604689489 cm.
Again, c is the radius of the ascribed half circle.
Calculating r, radius of the inscribed circle.
j = c-b
And b = 2 cm.
j = 5.4604689489-2
j = 3.4604689489 cm.
k = c-r
k = (5.4604689489-r) cm.
It implies;
(5.4604689489-r)² = r²+3.4604689489²
29.8167211419-10.9209378978r+r² = r²+11.9748453463
17.8418757956 = 10.9209378978r
r = 17.8418757956/10.9209378978
r = 1.6337310918 cm.
Again, r is the required length, the radius of the inscribed circle.