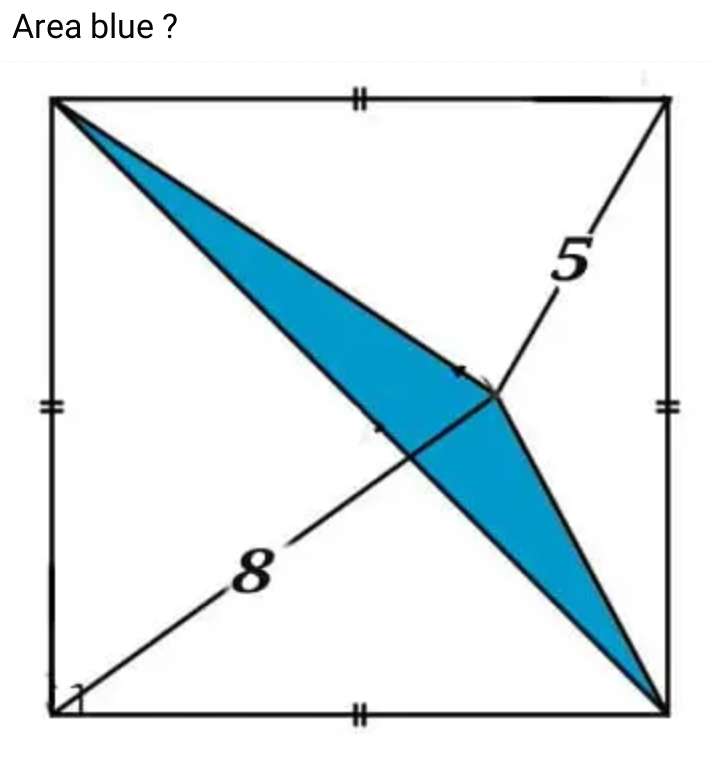
Mathematics Question and Solution
Let the side length of the square be a.
b²+(0.5a)² = 5²
b = √(25-¼(a²)) units.
c = a-b
c = (a-√(25-¼(a²))) units.
It implies, calculate a.
8² = (0.5a)²+(a-√(25-¼(a²)))²
64 = ¼(a²)+a²-2a√(25-¼(a²))+25-¼(a²)
39 = a²-2a√(25-¼(a²))
2a√(25-¼(a²)) = a²-39
4a²(25-¼(a²)) = a⁴-78a²+1521
100a²-a⁴ = a⁴-78a²+1521
2a⁴-178a²+1521 = 0
Let p = a².
2p²-178p+1521 = 0
p²-89p = -(1521/2)
(p-½(89))² = -(1521/2)+(-0.5*89)²
(p-44.5)² = 1219.75
p = 44.5±√(1219.75)
p ≠ 44.5-√(1219.75)
p = 44.5+√(1219.75)
p = 79.4249194702 units.
And a² = p.
It implies;
a = √(p)
a = √(79.4249194702)
a = 8.9120659485 units.
Again, a is the side length of the square.
d² = 2a²
d = √(2*8.9120659485²)
d = 12.6035645331 units.
d is the diagonal of a square.
cose = (0.5*8.9120659485/5)
e = 26.9747391928°
f = 45-e
f = 18.0252608072°
Therefore, area blue is;
0.5*5*12.6035645331sin18.0252608072
= 9.75 square units.