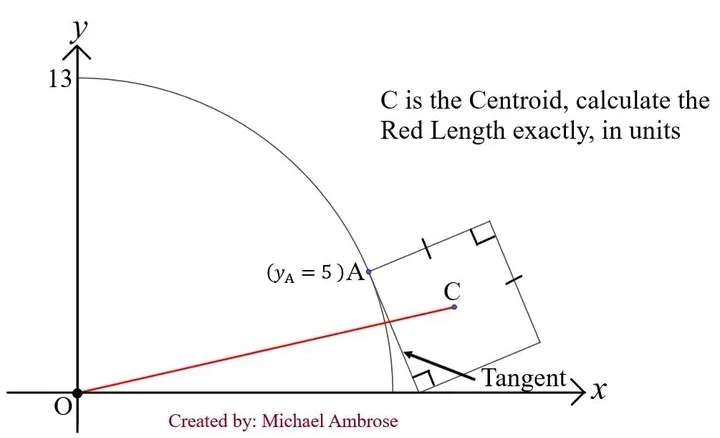
Mathematics Question and Solution
Let a be the side length of the square.
b² = 13²+a²
b = √(169+a²) units.
c² = 2a²
c = √(2)a units.
d²+5² = a²
d = √(a²-25) units.
e = b-d
e = (√(169+a²)-√(a²-25)) units.
Calculating a.
13² = (√(169+a²)-√(a²-25))²+5²
169-25 = (√(169+a²)-√(a²-25))²
144 = (√(169+a²)-√(a²-25))²
12 = (√(169+a²)-√(a²-25))
(12+√(a²-25))² = 169+a²
144+24√(a²-25)+a²-25 = 169+a²
144+24√(a²-25) = 194
24√(a²-25) = 50
12√(a²-25) = 25
144(a²-25) = 625
144a² = 625+(144*25)
144a² = 4225
a = √(4225/144)
a = 65/12 units.
a = 5.4166666667 units.
Again, a is the side length of the square.
Recall.
b = √(169+a²)
And a = (65/12) units.
b = √(169+(65/12)²)
b = (169/12) units.
b = 14.0833333333 units.
tanf = 13/(65/12)
f = atan(156/65)°
g = 45+f
g = (45+atan(156/65))°
Recall again.
c = √(2)a
And a = 65/12 units.
c = 65√(2)/12 units.
c = 7.6603234629 units.
c is the diagonal of the square.
h = ½(c)
h = 65√(2)/24 units.
h = 3.8301617314 units.
Therefore, red length, length OC exactly in decimal is;
Let it be j.
j² = 3.8301617314²+14.0833333333²-2*3.8301617314*14.0833333333cos(45+atan(156/65))
j = 15.9401005503 units.
Again, j is the required red length, length OC.