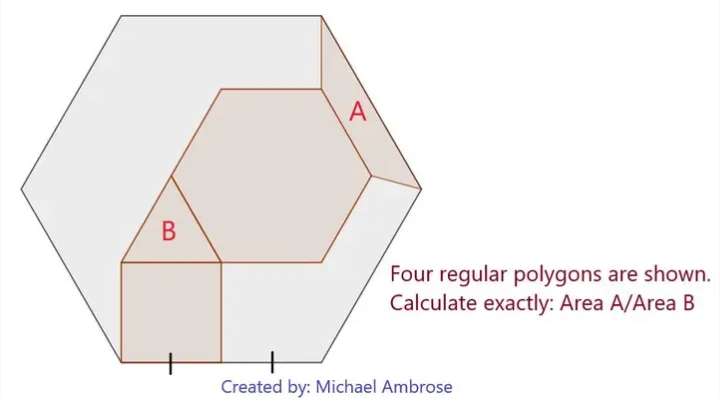
Mathematics Question and Solution
Let the side length of the ascribed regular hexagon be 2 units.
Calculating Area B.
½*1*1sin60
= ¼√(3) square units.
a = ⅙*180(6-2)
a = 120°
a is the single interior angle of the ascribed and inscribed regular hexagon.
b² = 2-2cos120
b = √(3) units.
c² = 2²+2²-2*2*2cos120
c² = 12
c = 2√(3) units.
d = c-b-1
d = 2√(3)-√(3)-1
d = (√(3)-1) units.
sin30 = e/(√(3)-1)
e = ½(√(3)-1) units.
Calculating Area A.
½(1+2)*½(√(3)-1)
= ¼(3√(3)-3) square units.
Therefore;
Area A ÷ Area B exactly is;
(¼(3√(3)-3))/(¼√(3))
= (3√(3)-3)/(√(3))
= ⅓(9-3√(3))
= 3-√(3)
= 1.2679491924