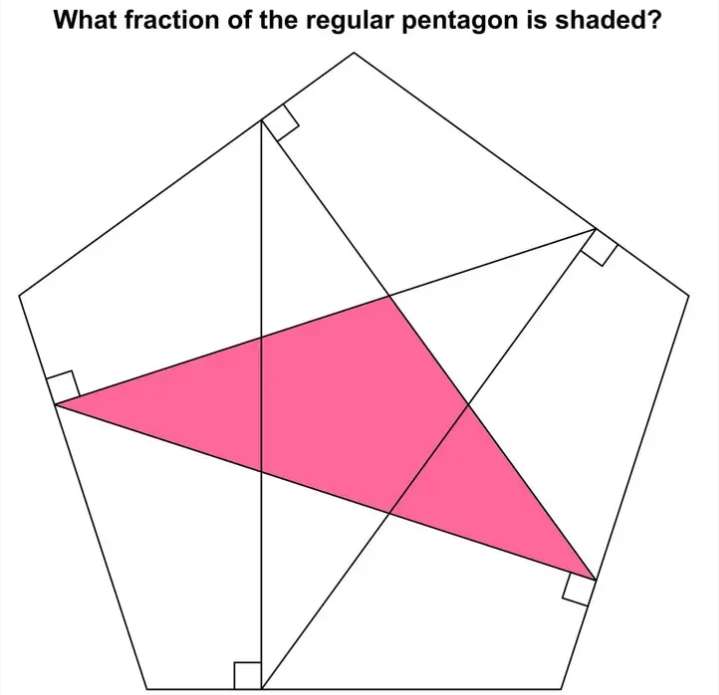
Mathematics Question and Solution
a = ⅕*180(5-2)
a = 108°
a is the single interior angle of the ascribed regular pentagon.
b = 360-2a-90
b = 360-306
b = 54°
c = 90-b
c = 36°
d = 180-2c
d = 108°
Notice.
The inscribed red triangle is isosceles. Let the two equal lengths be 1 unit each.
Area red inscribed isosceles triangle is;
0.5*1*1sin108
= 0.4755282581 square units.
Calculating area ascribed regular pentagon.
e² = 1²+1²-2*1*1cos108
e = 1.6180339887 units.
f = e-1
f = 0.6180339887 units.
g² = 0.6180339887²+0.6180339887²-2*0.6180339887*0.6180339887cos108
g = 1 unit.
h = 90-36
h = 54°
j = 72-54
j = 18°
(1/sin108) = (k/sin54)
k = 0.8506508084 units.
(1/sin108) = (l/sin18)
l = 0.3249196962 units.
m = k+l
m = 1.1755705046 units.
m is the side length of the ascribed regular pentagon.
o² = 1.1755705046²+1.1755705046²+2*1.1755705046*1.1755705046cos108
o = 1.9021130326 units.
sin72 = p/1.9021130326
p = 1.8090169944 units.
Therefore, area ascribed regular pentagon is;
2(0.5*1.1755705046²sin108)+(0.5*1.1755705046*1.8090169944)
= 1.3143277803+1.0633135105
= 2.3776412908 square units.
Therefore, the fraction of the regular shaded pentagon is;
Area inscribed red isosceles triangle ÷ Area ascribed regular pentagon.
= 0.4755282581/2.3776412908
= 0.2
= ⅕