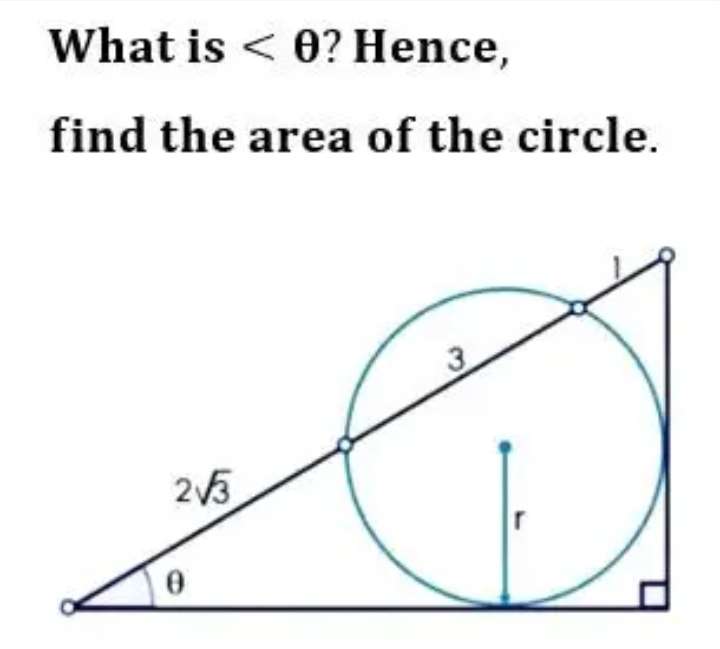
Mathematics Question and Solution
a = r+r
a = 2r units.
a is the diameter of the circle.
b = 3+1
b = 4 units.
c²+(2r)² = 4²
c = √(16-4r²) units.
It implies;
2√(3) - 4
r - √(16-4r²)
Cross Multiply.
4r = 2√(3(16-4r²))
2r = √(3(16-4r²))
4r² = 3(16-4r²)
4r² = 48-12r²
16r² = 48
r = √(3) units.
Therefore, area circle is;
πr²
= π√(3)²
= 3π square units.
Calculating the required angle, theta.
Let it be x.
c = √(16-4r²)
And r = √(3) units.
c = √(16-4√(3)²)
c = √(16-12)
c = √(4)
c = 2 units.
d = r+c
d = (2+√(3)) units.
e = 1+3+2√(2)
e = (4+2√(2)) units.
It implies;
sinx = d/e
x = asin((2+√(3))/(4+2√(2)))
x = asin(½)
x = 30°
Again, x is the required angle, theta.