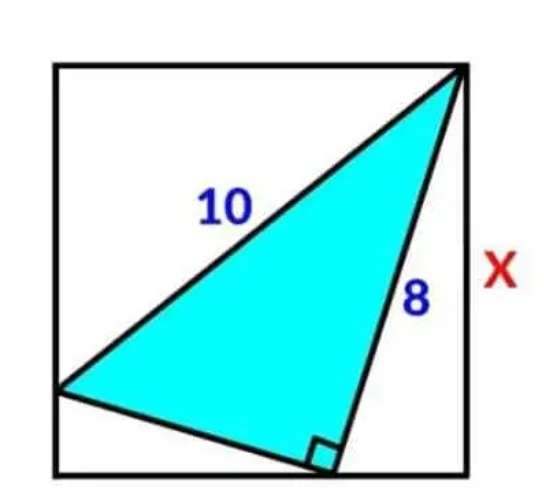
Mathematics Question and Solution
Calculating area of the ascribed square and area of the inscribed blue triangle.
a²+8² = 10²
a = 6 units.
6 - 8
b - x
Cross Multiply.
8b = 6x
b = ¼(3x) units
c²+x² = 8²
c = √(64-x²) units.
It implies;
b+c = x
¼(3x)+√(64-x²) = x
√(64-x²) = ¼(x)
64-x² = x²/16
(64*16)-16x² = x²
17x² = (64*16)
x = √((64*16)/17)
x = 32/√(17)
x = (32√(17))/17 units.
x = 7.7611400012 units.
x is the side length of the ascribed square.
Therefore, area of the ascribed square (x²) is;
x²
= ((32√(17))/17)²
= 1024/17 square units.
= 60.2352941176 square units.
Blue Area is;
½*6*8
= 24 square units.