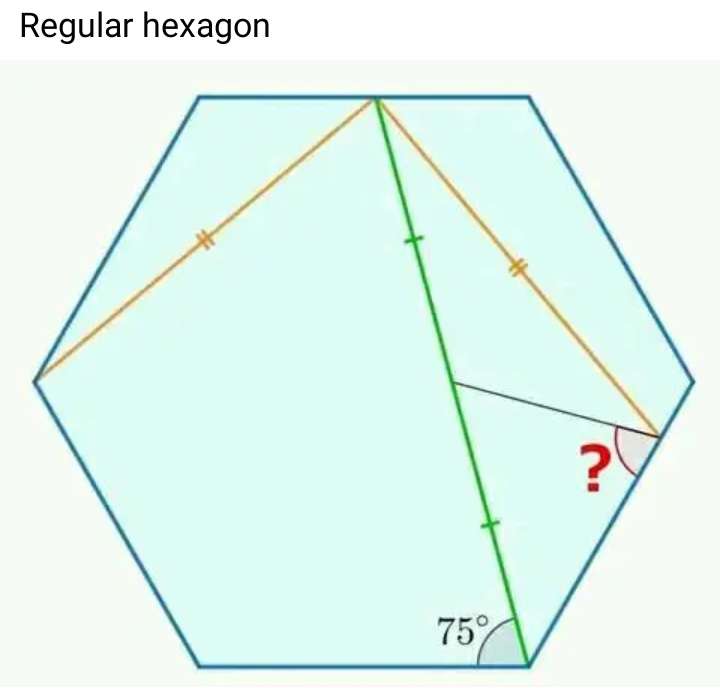
Mathematics Question and Solution
Let the height of the regular hexagon be 1 unit.
tan75 = 1/a
a = 0.2679491924 units.
sin75 = 1/b
b = 1.0352761804 units.
c = ½(b)
c = 0.5176380902 units.
1 = 2d²-2d²cos120
d is the side length of the regular hexagon while 120° is the single interior angle of the regular hexagon.
1 = 3d²
d = ⅓√(3) units.
d = 0.5773502692 units.
e = 75-30
e = 45°
f² = 1²+1.0352761804²-2*1*1.0352761804cos45
f = 0.7795480451 units.
(0.7795480451/sin45) = (1/sing)
g = 65.1039093617°
h = 90-g
h = 24.8960906383°
j² = 0.7795480451²+0.5176380902²-2*0.5176380902*0.7795480451cos24.8960906383
j = 0.378937382 units.
k = 120-75
k = 45°
Therefore, the required angle, ? is;
Let it be l.
(0.5176380902/sinl) = (0.378937382/sin45)
l = 75°