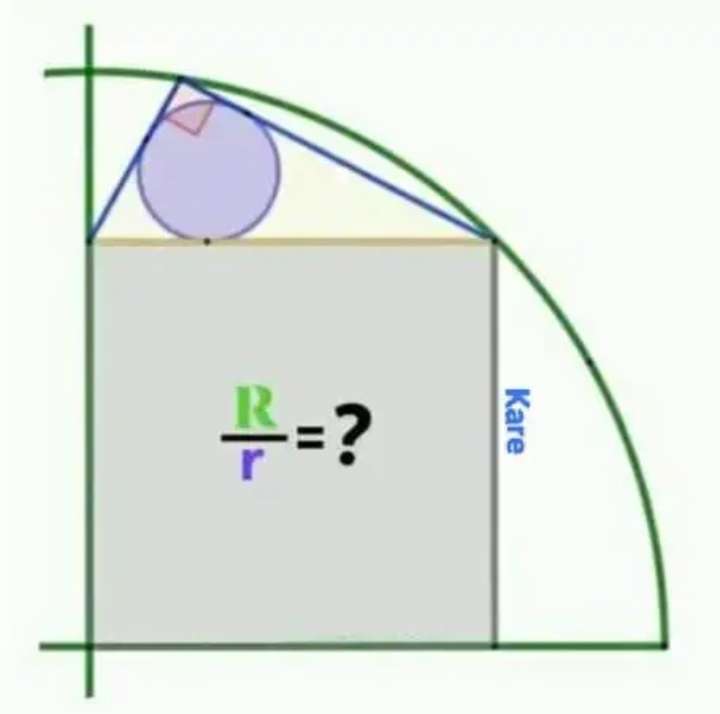
Mathematics Question and Solution
Let the radius of the ascribed quarter circle be 1 unit.
It implies;
R = 1 unit.
2a² = 1²
a² = ½
a = ½√(2) units.
a is the side length of the inscribed square.
b = 2R
b = 2 units.
b is the diameter of the complete circle.
c² = 2²+(½√(2))²-2*2*½√(2)cos45
c² = 4+½-2
c = √(5/2)
c = ½√(10) units.
c = 1.5811388301 units.
(1.5811388301/sin45) = (2/sind)
d = 63.4349488229°
sin63.4349488229 = e/(0.5√(2))
e = 0.632455532 units.
cos63.4349488229 = f/(0.5√(2))
f = 0.316227766 units.
Calculating r, radius of the inscribed circle.
0.316227766r+0.632455532r+0.7071067812r = 0.316227766*0.632455532
1.6557900792r = 0.2
r = 0.2/1.6557900792
r = 0.1207882584 units.
Again, r is the radius of the inscribed circle.
Therefore;
R/r is;
1÷0.1207882584
= 8.2789503969