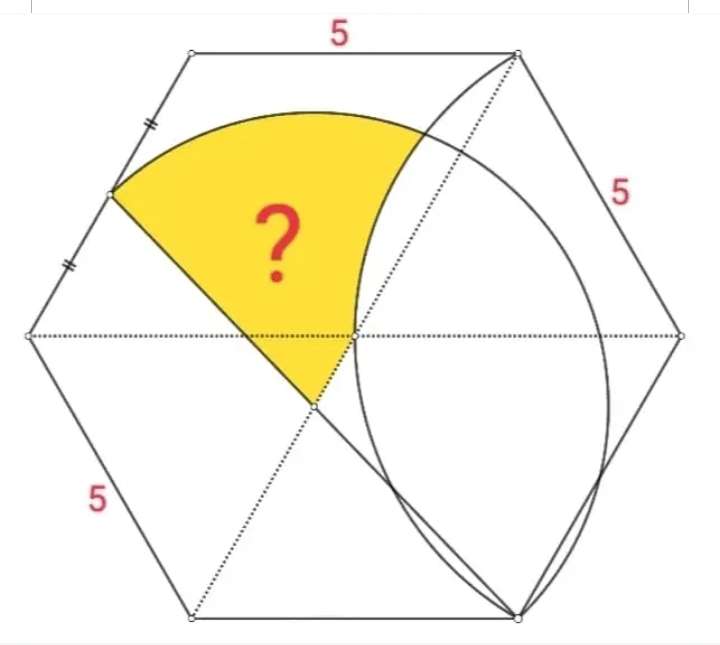
Mathematics Question and Solution
Calculating yellow area.
a² = 5²+5²-2*5*5cos120
120° is the single interior angle of the regular hexagon.
a = 5√(3) units.
a = 8.6602540378 units.
tanb = a/(2.5)
b = atan(5√(3)/(5/2))
b = atan(2√(3))°
b = 73.897886248°
b is the angle of the yellow incomplete sector.
c² = 2.5²+(5√(3))²
c = 8.6746757864 units.
d = ½(c)
d = 4.3373378932 units.
d is the radius of the yellow incomplete sector.
e = 90-atan(2.5/(5√(3)))
e = 73.897886248°
f² = 4.33733789322+5²-2*5*4.3373378932cos73.897886248
f = 5.6376315149 units.
(5.6376315149/sin73.897886248) = (4.3373378932/sing)
g = 47.6609317741°
5² = 4.3373378932²+5.6376315149²-2*5.6376315149*4.3373378932cosh
25.5953890976/48.9046255949 = cosh
h = 58.4411819776°
j = h-g
j = 10.7802502035°
k² = 2(4.3373378932)²-2(4.3373378932)²cos10.7802502035
k = 0.814870654 units.
l = ½(180-10.7802502035)
l = 84.6098748983°
(5/sin(180-73.897886248)) = (4.3373378932/sinm)
m = 56.4533220414°
n = 180-m-(180-73.897886248)
n = 17.4445642066°
(5/sin(180-73.897886248)) = (o/sin17.4445642066)
o = 1.5601196876 units.
p = d-o
p = 2.7772182056 units.
q² = 2.7772182056²+0.814870654²-2*0.814870654*2.7772182056cos84.6098748983
q = 2.8198907223 units.
2.8198907223² = 50-50cosr
50cosr = 42.0482163143
r = 32.7579093794°
Therefore, yellow area is;
(73.897886248π*4.3373378932²/360)-(0.5*2.7772182056*0.814870654sin84.6098748983)-(32.7579093794πx5²/360)+(0.5*5*5sin32.7579093794)
= 12.1318184065-1.1265333436-7.1466671843+6.76363209
= 10.6222499686 square units.