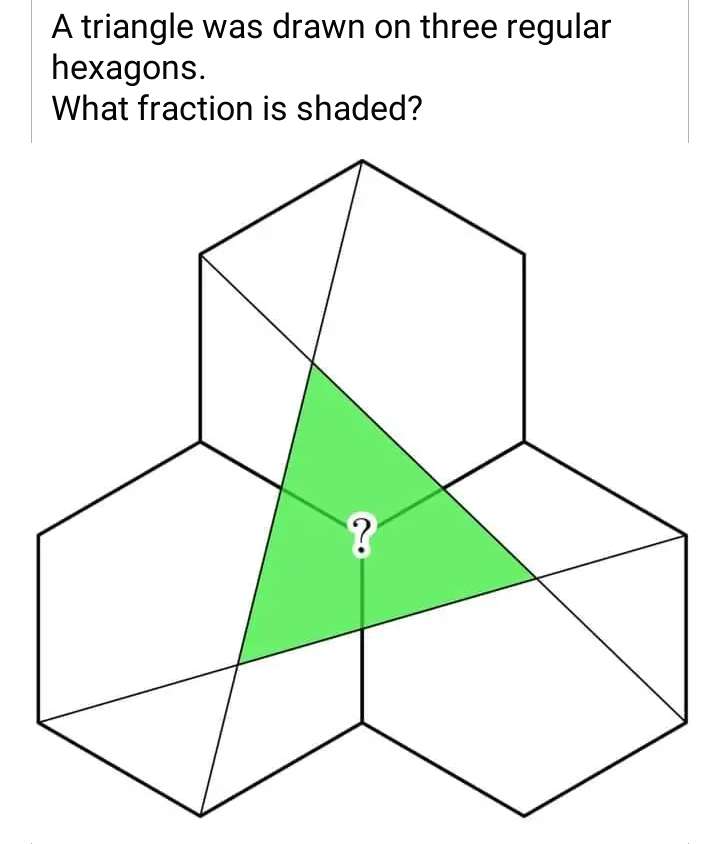
Mathematics Question and Solution
Let the side length of the three congruent regular hexagon be 1 unit each.
Notice.
The inscribed green triangle is equilateral.
a² = 2-2cos120
120° is the single interior angle of one of the congruent regular hexagon.
a = √(3) units.
b = 2a
b = 2√(3) units.
c² = (2√(3))²+1²
c² = 13
c = √(13) units.
tand = 2√(3)/1
d = atan(2√(3))°
e = atan(1/(2√(3)))°
f = 120-d
f = 46.102113752°
It implies;
(1/sin60) = (g/sin(atan(2√(3)))
g = 1.1094003925 units.
(1/sin60) = (h/sin(46.102113752))
h = 0.8320502943 units.
Therefore;
j = c-g-h
j = √(13)-1.1094003925-0.8320502943
j = 1.6641005886 units.
j is the side length of the inscribed green equilateral triangle.
Area inscribed green equilateral triangle is;
0.5*1.6641005886²sin60
= 1.1991120974 square units.
Calculating the area of the three congruent regular hexagon.
It is;
3(2(0.5*1²*sin60)+(√(3)*1))
= 3(½√(3)+√(3))
= 3(½(3√(3)))
= ½(9√(3)) square units.
= 7.7942286341 square units.
Therefore;
Shaded Fraction is;
Area green inscribed equilateral triangle ÷ Area of the three congruent regular hexagon
=1.1991120974÷7.7942286341
= 0.1538461538