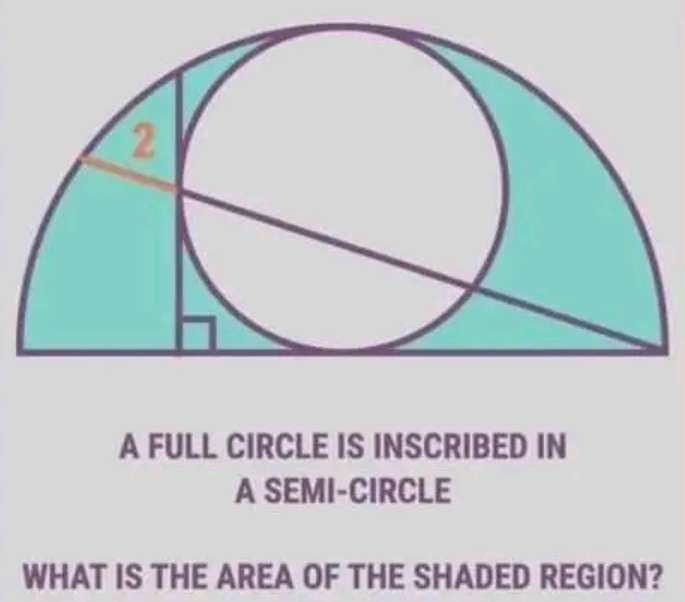
Mathematics Question and Solution
Let the radius of the semi circle be r.
Calculating r.
2+√(5/2)r - ½(3r)
2r - √(5/2)r
Cross multiply.
3r² = 2√(5/2)r + (5/2)r²
(½)r² = 2√(5/2)r
(¼)r² = √(5/2)r
(1/16)r⁴ = (5/2)r²
(r²/16) = (5/2)
2r² = 80
r² = 40
r = √(40)
r = 2√(10) units.
Therefore radius, q of the inscribed circle is;
q = ½(r)
And r = 2√(10) units.
q = ½(2√(10))
q = √(10) units.
It implies shaded area will be;
Area ascribed semi circle with radius 2√(10) unit - Area inscribed circle with radius √(10) unit.
= ½π(2√(10))² - π(√(10))²
= ½(40π) - 10π
= 20π - 10π
= 10π square units.