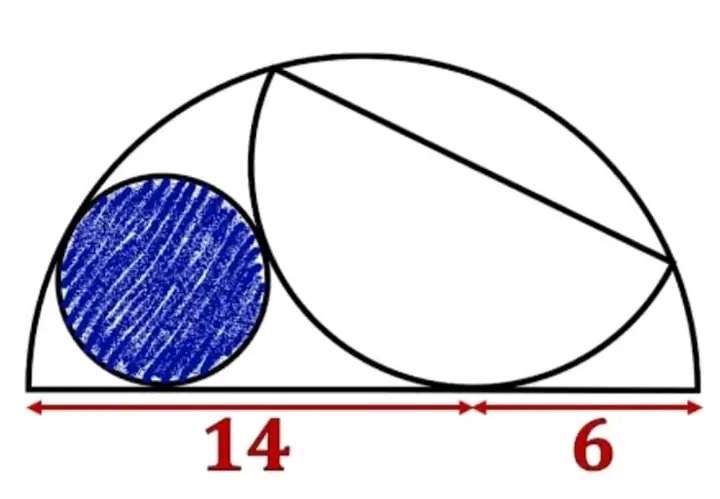
Mathematics Question and Solution
Calculating the area of the inscribed blue circle.
a = ½(14+6)
a = 10 units.
a is the radius of the ascribed semi circle.
b = a-6
b = 4 units.
c²+4² = d²
c is the radius of the inscribed half circle.
d = √(c²+16) units.
10² = √(c²+16)²+c²
100 = c²+16+c²
84 = 2c²
c² = 42
c = √(42) units.
Again, c is the radius of the inscribed half circle.
e = (c+f)
e = (√(42)+f) units.
f is the radius of the inscribed blue circle.
g = (10-f) units.
Notice!
d = √(c²+16)
And c = √(42) units.
d = √(42+16)
d = √(58) units.
It implies;
(10-f)²+√(58)² = (√(42)+f)²
100-20f+f²+58 = 42+2√(42)f+f²
158-20f = 42+2√(42)f
2(10+√(42))f = 116
(10+√(42))f = 58
f = 58/(10+√(42))
f = 3.5192593016 units.
Again, f is the radius of the inscribed blue circle.
Area inscribed blue circle is;
π(3.5192593016)²
= 38.909209451 square units.
= 38.91 square units.