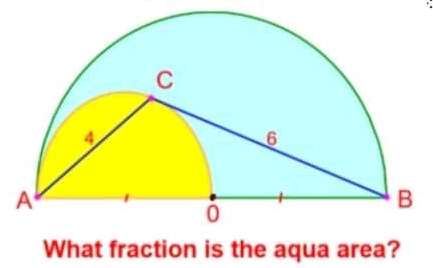
Mathematics Question and Solution
Let the radius of the ascribed semi circle be a.
b = ½(a) units.
c = b+a
c = ½(3a) units.
It implies;
(½(3a))² = (½a)²+6²
¼(9a²) = ¼(a²)+36
¼(8a²) = 36
8a² = 36*4
a² = 18
a = 3√(2) units.
Again, a is the radius of the ascribed semi circle.
b = ½(a)
b = ½(3√(2)) units.
b is the radius of the inscribed yellow half circle.
Area inscribed yellow circle is;
½(½(3√(2)))²π
= ⅛(18)π
= ¼(9π) square units.
Area ascribed semi circle is;
½(3√(2))²π
= 9π square units.
The shaded fraction of the aqua area is;
(Area ascribed semi circle - Area inscribed yellow circle) ÷ Area ascribed semi circle
= (9π-¼(9π))/9π
= (¼(27π))/9π
= ¾
= 0.75