Mathematics Question and Solution
Notice!
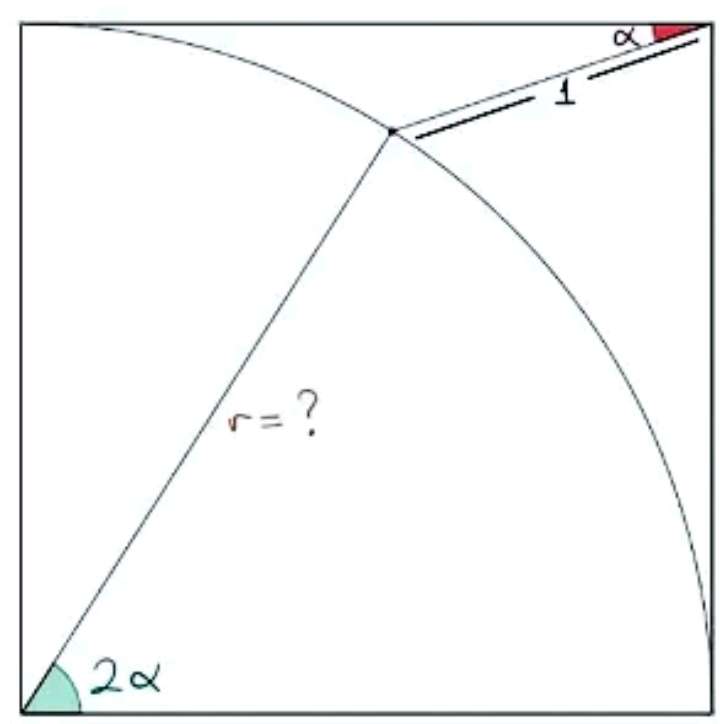
r, radius of the inscribed quarter circle is also the side length of the ascribed square.
Let alpha be a.
Notice again.
2a = 60°
a = 30°
Alpha = 30°
It implies;
sin30 = b/1
b = ½ units.
c = (r-½) units.
d = ½(r) units.
Calculating r, radius of the inscribed quarter circle and the side length of the ascribed square.
r² = (r-½)²+(½(r))²
r² = r²-r+¼+¼(r²)
¼(r²)-r+¼ = 0
r²-4r+1 = 0
Calculating the above quadratic equation via completing the square approach to get r, radius of the inscribed quarter circle and side length of the ascribed square.
(r-2)² = -1+(-2)²
(r-2)² = 3
r = 2±√(3)
It implies;
r ≠ (2-√(3)) units.
r = (2+√(3)) units.
r = 3.7320508076 units.