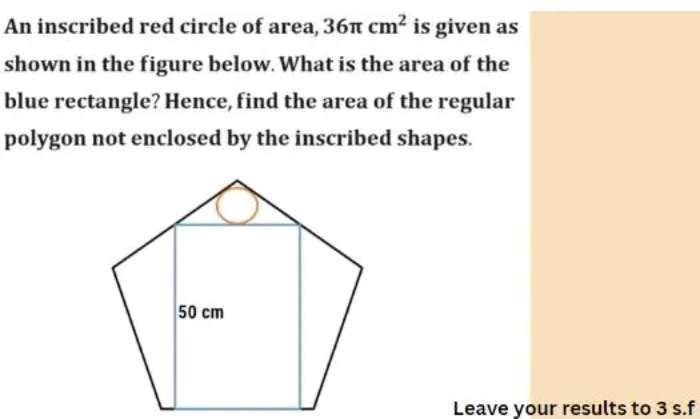
Mathematics Question and Solution
Calculating the area of the blue inscribed rectangle and the area of the ascribed regular pentagon.
πr² = 36π
r = 6 cm.
r is the radius of the inscribed circle.
sin(0.5*108) = 6/a
a = 7.416407865 cm.
b = r+a
b = 13.416407865 units.
tan36 = 13.416407865/c
c = 18.4661012231 cm.
d = 2c
d = 36.9322024461 cm.
d is the width of the inscribed blue rectangle.
Therefore;
Area Blue Inscribed Rectangle is;
36.9322024461*50
= 1846.6101223052 cm²
≈ 1850 cm² to 3 significant figures.
Calculating area of the ascribed regular pentagon.
e = b+50
e = 13.416407865+50
e = 63.416407865 cm.
tan18 = f/63.416407865
f = 20.6052399797 cm.
g = 2f
g = 41.2104799594 cm.
g is the side length of the ascribed regular pentagon.
Therefore, area ascribed regular pentagon is;
2(½*41.2104799594²sin108)+(½*41.2104799594*63.416407865)
= 2921.8930637581 cm²
≈ 2920 cm² to 3 significant figures.