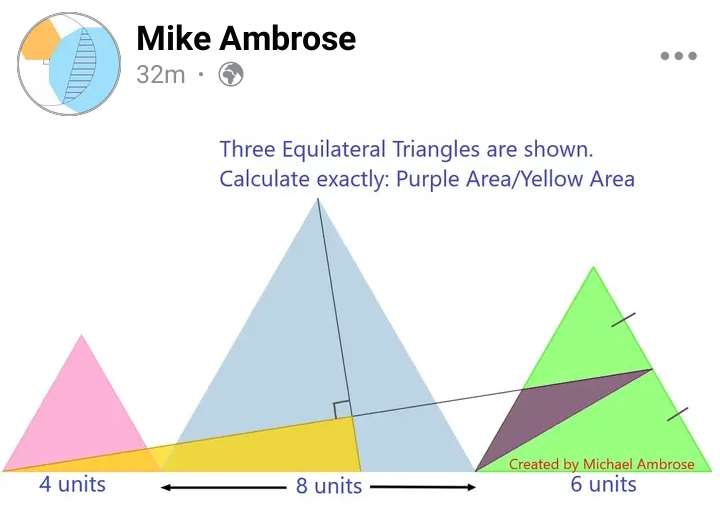
Mathematics Question and Solution
Let the green and purple color regular triangle side be a.
b = √(4²+2²)
b = 2√(5) units.
c = 0.5b
c = √(5) units.
d = √(8²+4²)
d = 4√(5) units.
e = √(a²+(a/2)²)
e = √(5a²/4)
e = ½(√(5)a)
Calculating a, side length of the green and purple regular triangle.
d-c = e
4√(5)-√(5) = ½(√(5)a)
3√(5) = ½(√(5)a)
3 = ½(a)
a = 6 units.
sin60 = f/3
f = ½(3√(3)) units.
cos60 = g/3
g = (3/2) units.
h = 6-(3/2)
h = (9/2) units.
j = 12+(9/2)
j = (33/2) units.
tank = (3√(3)/2)/(33/2)
k = atan(√(3)/11)°
k = 8.94827556463°
l² = 8²-4²
l = √(48)
l = 4√(3) units
(√(3)/11) = m/(4√(3))
m = (12/11) units.
n = 8+(12/11)
n = (100/11) units.
sin(atan(√(3)/11)) = o/(100/11)
o = (50√(93)/341) units.
cos(atan(√(3)/11)) = p/(100/11)
p = (50√(31)/31) units.
Area yellow is;
0.5*(50√(93)/341) (50√(31)/31)
= (1250√(3)/341) square units.
Calculating Area Purple.
q = √(6²-3²)
q = √(27)
q = 3√(3) units.
r = (30-atan(√(3)/11))°
s = 180-30-(30-atan(√(3)/11)
s = (120+atan(√(3)/11))°
(3√(3)/sin(120+atan(√(3)/11)) = (t/sin(30-atan(√(3)/11)))
t = 2.4 units.
t = (12/5) units.
Area Purple is;
0.5*(12/5)*3√(3)sin30
= (9√(3)/5) square units.
It implies;
Area Purple ÷ Area Yellow exactly is;
(9√(3)/5)÷(1250√(3)/341)
= 3069/6250