Mathematics Question and Solution
Notice!
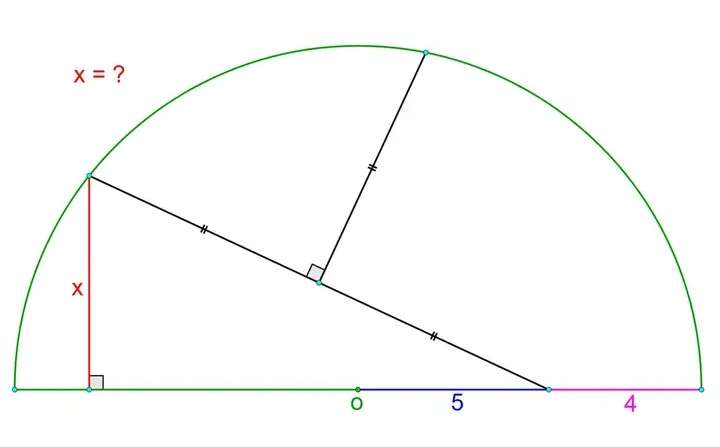
Radius of the half circle is 9 units.
Let the three equal lengths be b.
5² = b²+a²-2bacos45
25 = b²+a²-√(2)ab --- (1).
9² = b²+a²-2abcos135
81 = b²+a²+√(2)ab --- (2).
Subtracting (1) from (2).
56 = 2√(2)ab
28 = √(2)ab
a = 28/(√(2)b) --- (3).
Substituting (3) in (2) to get b.
81 = b²+(28/(√(2)b))²+√(2)(28/(√(2)b))b
81 = b²+(392/b²)+28
53 = b²+(392/b²)
53b² = b⁴+392
Let b² = p.
p²-53p +392 = 0
Calculating p.
It implies;
p = ½(53+√(1241))
p = 44.11391
And b² = p
Therefore;
b = √(44.11391)
b = 6.64183032 units.
a = 28/(√(2)b)
And b = 6.64183032 units.
a = 28/(6.64183032√(2))
a = 2.9809538816 units.
(5/sin45) = (2.9809538816/sinc)
c = 24.9337820662°
It implies, length x is;
sin24.9337820662 = x/(2*6.64183032)
x = 5.6 units.
x = ⅕(28) units.