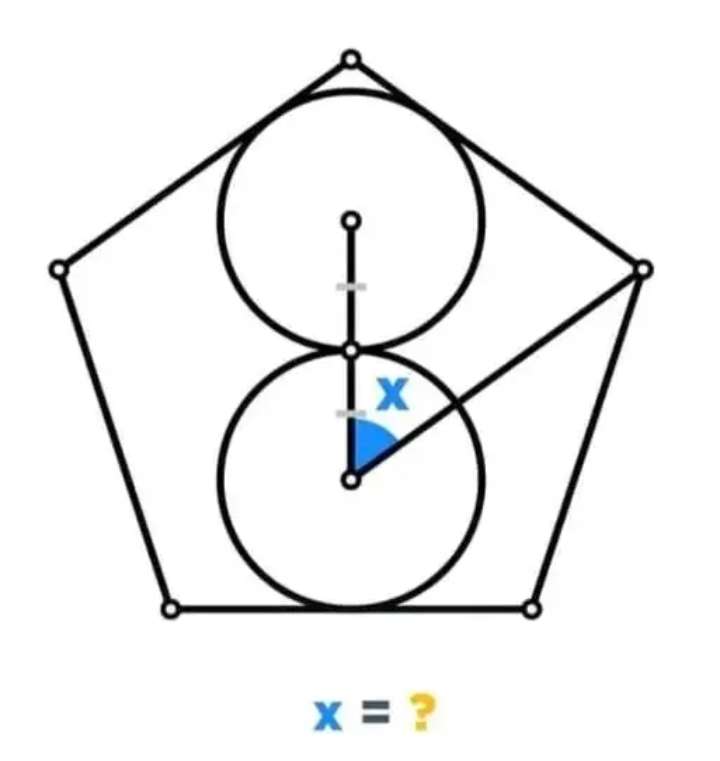
Mathematics Question and Solution
Calculating angle x.
Let the side length of the regular pentagon be 1 unit.
Calculating r, radius of the inscribed two equal circles.
a = ⅕*180(5-2)
a = 108°
b = ½(a)
b = ½*108
b = 54°
sin54 = r/c
c = r/(sin54) units.
c = 1.2360679775r units.
d = 108-½(180-108)
d = 108-36
d = 72°
tan72 = e/0.5
e = 1.5388417686 units.
It implies;
3r+c = e
3r+1.2360679775r = 1.5388417686
4.2360679775r = 1.5388417686
r = 0.363271264 units.
Again, r is the radius of each of the inscribed two equal circles.
tanf = 0.5/r
f = atan(0.5/0.363271264)
f = 54°
g = 90-f
g = 90-54
g = 36°
sin54 = 0.5/h
h = 0.6180339887 units.
j = 108-g
j = 108-36
j = 72°
k² = 0.6180339887²+1-2*0.6180339887cos72
k = 1 unit.
Therefore, the required angle x is;
x = 180-54-72
x = 180-126
x = 54°