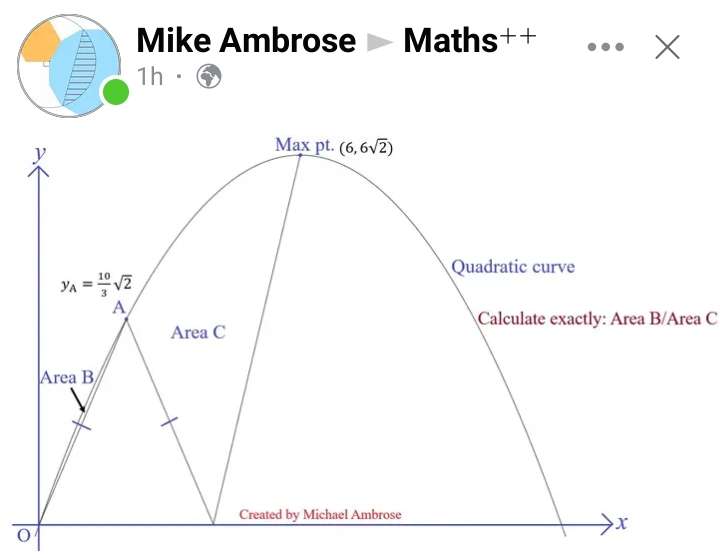
Mathematics Question and Solution
Calculating equation of the curve.
y-6√(2) = a(x-6)² --- (1).
Substituting x = 0, y = 0 to get a.
It implies;
-6√(2) = 36a
a = -(1/(3√(2)) --- (2).
Substituting (2) in (1).
y-6√(2) = -(1/(3√(2))(x-6)²
y = -(1/(3√(2))(x²-12x+36)+6√(2)
y = -(x²/(3√(2))+2√(2)x-6√(2)+6√(2)
y = -(x²/(3√(2))+2√(2)x --- (3).
Where (3) is the equation of the curve.
Calculating x, when y is ⅓(10√(2)).
⅓(10√(2)) = -(x²/(3√(2))+2√(2)x
(x²/(3√(2))-2√(2)x+⅓(10√(2)) = 0
x²-12x+20 = 0
Resolving the quadratic equation.
(x-6)² = -20+(-6)²
(x-6)² = -20+36
x = 6±√(16)
x = 6±4
Therefore;
x ≠ 10
x = 2.
Calculating Area B.
It is;
(Area under the curve at x = 0 and x = 2)-Area triangle with height and base ⅓(10√(2)) units and 2 units respectively.
= ⅑(32√(2))-0.5(2*⅓(10√(2)))
= ⅑(32√(2))-⅓(10√(2))
= ⅑(32√(2)-30√(2))
= ⅑(2√(2)) square units.
Calculating Area C.
It is;
(Area under the curve at x = 2 and x = 6)-Area triangle with height and base ⅓(10√(2)) units and 2 units respectively-Area triangle with height and base 6√(2) units and 2 units respectively.
= ⅑(184√(2))-0.5(2*⅓(10√(2))-0.5(2*6√(6))
= ⅑(184√(2))-⅓(10√(2))-6√(2)
= ⅑(184√(2)-30√(2)-54√(2))
= ⅑(184√(2)-84√(2))
= ⅑(100√(2)) square units.
Therefore;
Area B÷Area C Exactly is;
⅑(2√(2))÷⅑(100√(2))
= 1/50