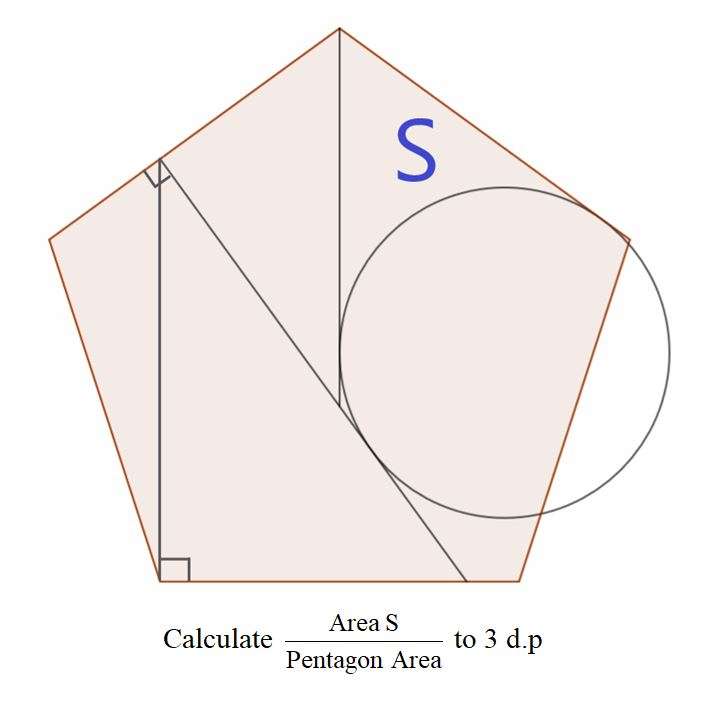
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the side of the regular pentagon be 1 unit.
Area regular pentagon is;
½(5)*(1/(2tan(36)))
= 1.72047740059 square units.
a = ⅕(180*3)
a = 108°
(1/sin54) = (b/sin18)
b = 0.38196601125 unit.
c = 1-b
c = 0.61803398875 unit.
sin36 = (0.61803398875/d)
d = 1.05146222424 units.
e = asin(0.61803398875/1.05146222424)
e = 36°
(f/sin27) = (1.05146222424/sin81)
f = 0.48330413656 unit.
Le the radius of the circle be r.
sin72 = r/0.48330413656
r = 0.45964954843 unit.
tan72 = 0.45964954843/g
g = 0.14934919165 unit.
h = 1.05146222424-g
h = 0.90211303259 unit.
Area S is;
2(½*0.90211303259*0.45964954843) - (126*0.45964954843²*π÷360)
= 0.41465584806 - 0.23231197267
= 0.18234387539 square units.
Therefore;
Area S ÷ Area Pentagon to 3 decimal places is;
0.18234387539 ÷ 1.72047740059
= 0.10598446415
≈ 0.106