Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
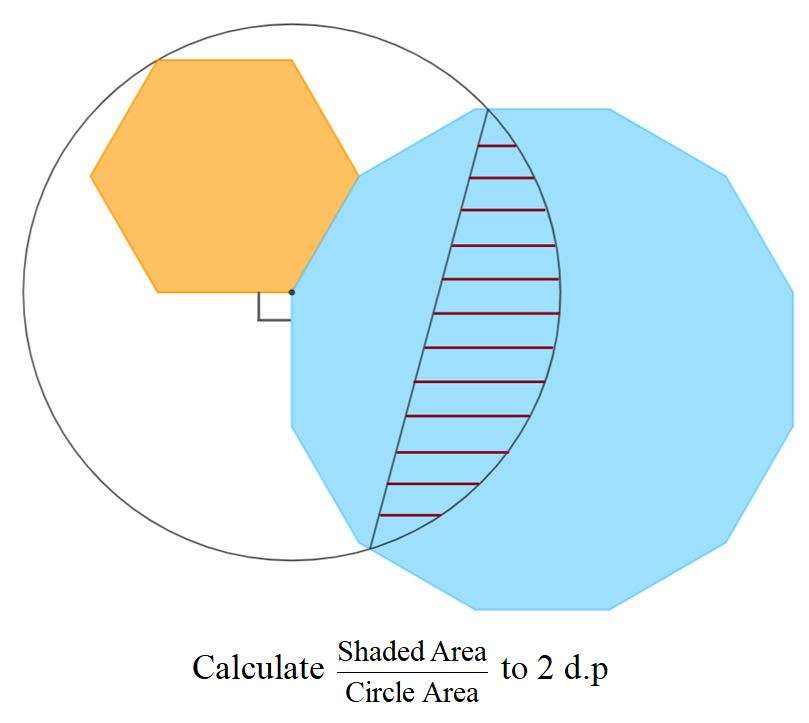
Let the side length of the inscribed regular hexagon be 1 unit.
Calculating r, radius of the circle.
1+2(sin30)
r = 2 units.
Area circle is;
π(2)²
= 4π square units.
= 12.56637061436 square units.
a = (1800/12)
a = 150°
b² = 2-2cos150
b = 1.93185165258 units.
2² = c²+1.93185165258²-2*1.93185165258*ccos135
4 = c²+3.73205080758+ 2.73205080757c
c²+2.73205080757c-0.26794919242 = 0
c = 0.0947876 unit.
(2/sin135) = (1.93185165258/sind)
d = 43.0795171417°
e = 75-d
e = 31.9204828583°
f = 180-2e
f = 116.1590342834°
Area Shaded is;
((116.1590342834)π*4÷360) - (2sin 116.1590342834)
= 4.05471520836 - 1.79514762218
= 2.25956758618 square units.
Therefore;
Area Shaded ÷ Area Circle to 2 decimal places is;
2.25956758618 ÷ 12.56637061436
= 0.1798106753
≈ 0.18