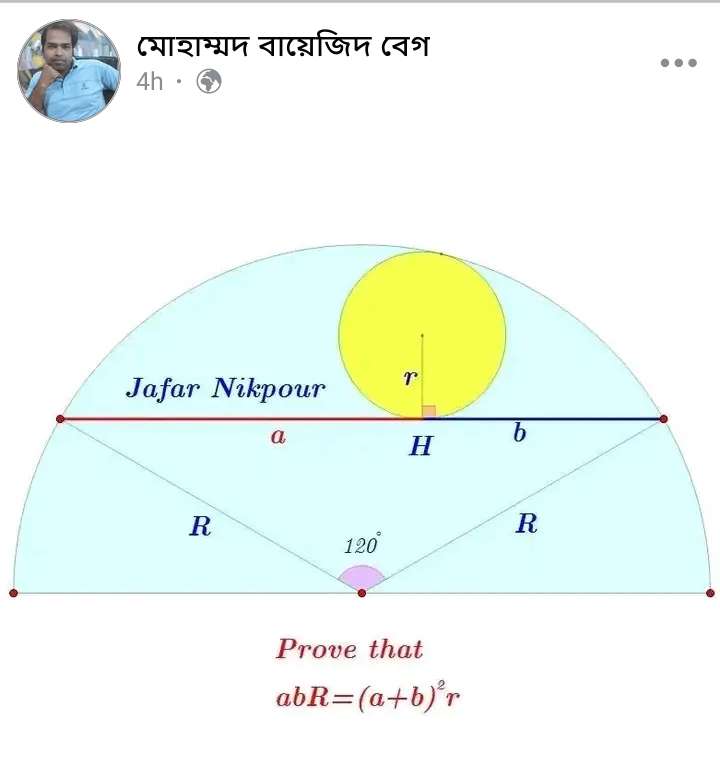
Mathematics Question and Solution
Let the radius R, of the half circle be 1 unit.
sin30 = c/1
c = ½ units.
c = 0.5 units.
cos30 = d/1
d = ½√(3) units.
d = 0.86602540378 units.
e = 1-0.86602540378
e = 0.13397459622 units.
f² = (0.13397459622)²+(0.5)²
f = 0.51763809021 units.
Calculating r, radius of the small inscribed yellow circle.
Considering similar triangle ratios.
0.51763809021 = (1-r)
0.5 = (0.5+r)
Cross Multiply.
0.5-0.5r = 0.51763809021r+0.2588190451
0.5-0.2588190451 = 0.5r+0.51763809021r
0.2411809549 = 1.01763809021r
r = 0.23700071491 units.
g = 1-0.23700071491
g = 0.76299928509 units.
h = 0.5+0.23700071491
h = 0.73700071491 units.
j²+0.73700071491² = 0.76299928509²
j = 0.19747874638 units.
Calculating a and b.
k² = 2-2cos120
k = 1.73205080757 units.
l = 0.5k
l = 0.5*1.73205080757
l = 0.86602540378 units.
b = l-j
b = 0.86602540378-0.19747874638
b = 0.6685466574 units.
a = l+j
a = 0.86602540378+0.19747874638
a = 1.06350415016 units.
Therefore observing the proof.
abR = r(a+b)²
Notice;
R = 1 unit.
r = 0.23700071491 units.
a = 1.06350415016 units.
b = 0.6685466574 units.
It implies;
abR is;
1.06350415016*0.6685466574*1
= 0.71100214472 square units.
r(a+b)² is;
0.23700071491(1.06350415016+0.6685466574)²
= 0.71100214472 square units.
Proved!