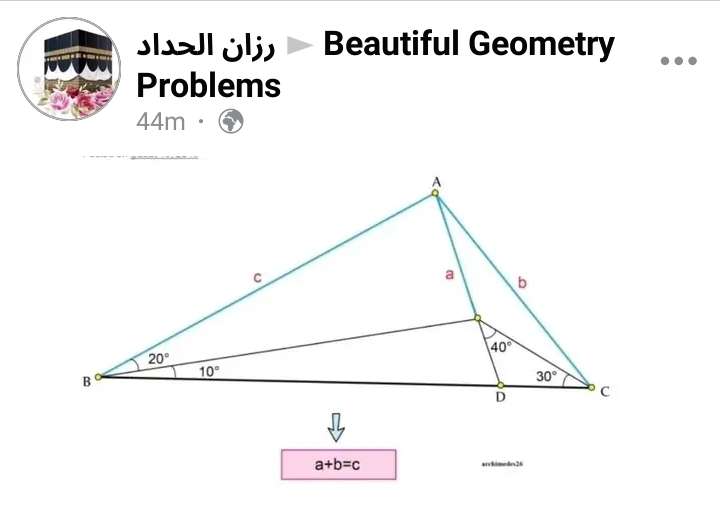
Mathematics Question and Solution
Let BD be 1 unit.
Therefore;
(1/sin100) = (d/sin70)
d = 0.95418889414 units.
(1/sin80) = (AB/sin70)
AB = 0.95418889414 units.
AB is c.
It implies;
d = c.
Calculating a.
(a/sin20) = (0.95418889414/sin80)
a = 0.33138632523 units.
Calculating b.
(1/sin100) = (e/sin10)
e = 0.17632698071 units.
(0.17632698071/sin30) = (f/sin110)
f = 0.33138632523 units.
It implies;
(0.33138632523/sin20) = (b/sin140)
b = 0.6228025689 units.
Confirming the proof;
a+b = c
Notice;
c = 0.95418889414 units.
a+b is;
a+b = 0.33138632523+0.6228025689
= 0.95418889413 units.
It implies;
a+b = c
Proved.