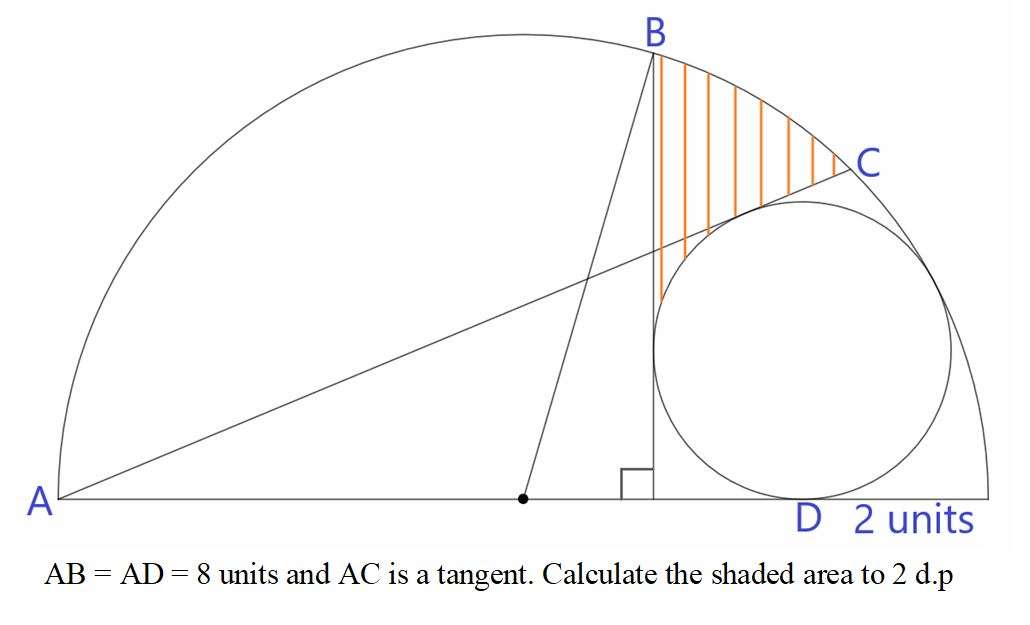
Mathematics Question and Solution
Radius of the semi circle is 5 units.
Calculating r, radius of the inscribed circle.
(5-r)² = 3²+r²
25-10r+r² = 9+r²
10r = 16
r = ⅕(8) units.
a = 3-r
a = ⅕(7) units.
b² = 5²-a²
b = ⅕(24) units.
c = atan((8/5)/8)
c = atan(⅕)°
d = 2c
d = 2atan(⅕)°
tan(2tan(⅕)) = e/(5+(7/5))
e = ⅓(8) units.
f = atan(12/5)°
g = b-f
g = (32/15) units.
h² = 50-50cos(180-4atan(⅕))
h = (120/13) units.
sin(2atan(⅕)) = (8/3)/i
i = (104/15) units.
j = h-i
j = (448/195) units.
k = atan(24/7)°
l = (180-atan(24/7))°
m = (180-4atan(⅕))-(180-atan(24/7))
m = (atan(24/7)-4ata(1/5))°
m = 28.50006539561°
n = (8/3)-(8/5)
n = (16/15) units.
o = 2atan((16/15)/(8/5))
o = 2tan(⅔)°
Therefore;
Area Shaded to 2 decimal places is;
½(32/15)(448/195)sin(atan(12/5)) + (28.50006539561π*25/360) - (½*25sin28.50006539561) + 2*½(8/5)(16/15) - (2atan(⅔)π*(8/5)²/360)
= 2.26209072978 + 6.21774972734 - 5.96449704142 + 1.70666666667 - 1.50528666508
= 2.71672341729 square units.
≈ 2.72 square units.