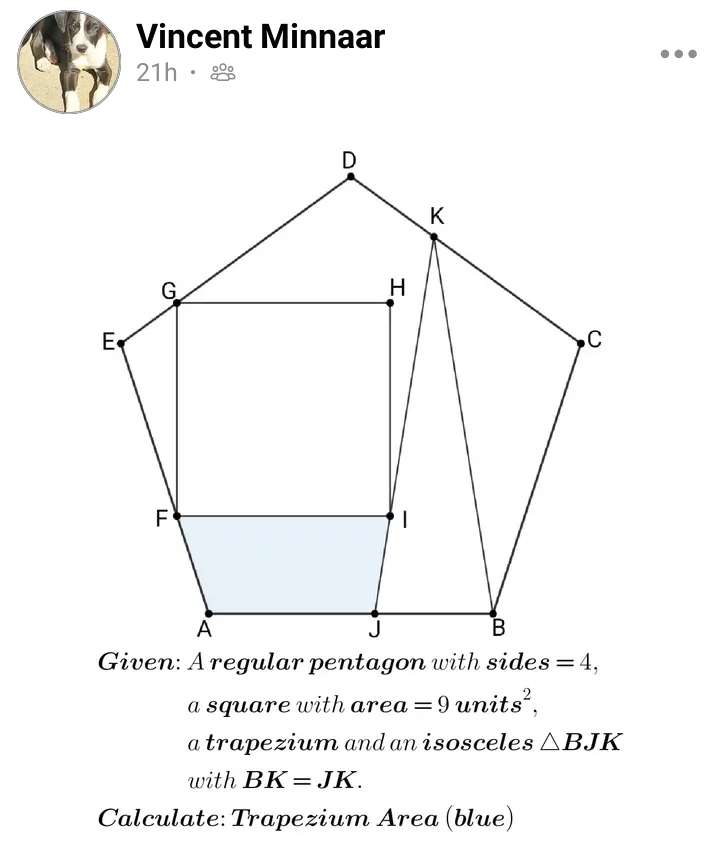
Mathematics Question and Solution
(3/sin108) = (EG/sin18)
EG = 0.9747590887 units.
(3/sin108) = (EF/sin54)
EF = 2.55195242506 units.
AF = 4-2.55195242506
AF = 1.44804757494 units.
sin18 = a/1.44804757494
a = 0.44747130932 units.
cos18 = b/1.44804757494
b = 1.37717508205 units.
b is the height of the trapezoid.
Let BJ be x.
c = (2-x) units.
d² = 1.44804757494²+2²-4*1.44804757494cos108
d = 2.80833171413 units.
(2.80833171413/sin108) = (2/sine)
e = 42.63384501172°
f = 72-42.63384501172
f = 29.36615498828°
g² = 3²+2.80833171413²-6*2.80833171413cos29.36615498828
g = 1.48387976624 units.
(1.48387976624/sin29.36615498828) = (3/sing1)
g1 = 82.49471818166°
g2 = 180-82.49471818166-29.36615498828
g2 = 68.13912683006°
h = 4-(3-0.44747130932)
h = 1.44747130932 units.
j = (x-1.44747130932) units.
k² = (x-1.44747130932)²+1.37717508205²
k² = x²-2.89494261864x+2.0951731913+1.89661120662
k = √(x²-2.89494261864x+3.99178439792) units.
k is IJ.
Therefore;
√(x²-2.89494261864x+3.99178439792)² = 1.44804757494²+(2-x)²-2*1.44804757494(2-x)cos72
(x²-2.89494261864x+3.99178439792) = 2.09684177929+4-4x+x²-0.89494261864(2-x)
-2.89494261864x+3.99178439792) = 6.09684177929-4x+0.89494261864x-1.78988523728
(4-0.89494261864-2.89494261864)x = 6.09684177929-3.99178439792-1.78988523728
0.21011476272x = 0.31517214409
x = 1.5 units.
And x is BJ.
AJ = AB-BJ
AJ = 4-1.5
AJ = 2.5 units.
Area Blue Trapezoid is;
0.5(3+2.5)*1.37717508205
= 0.5*5.5*1.37717508205
= 3.78723147564 square units.