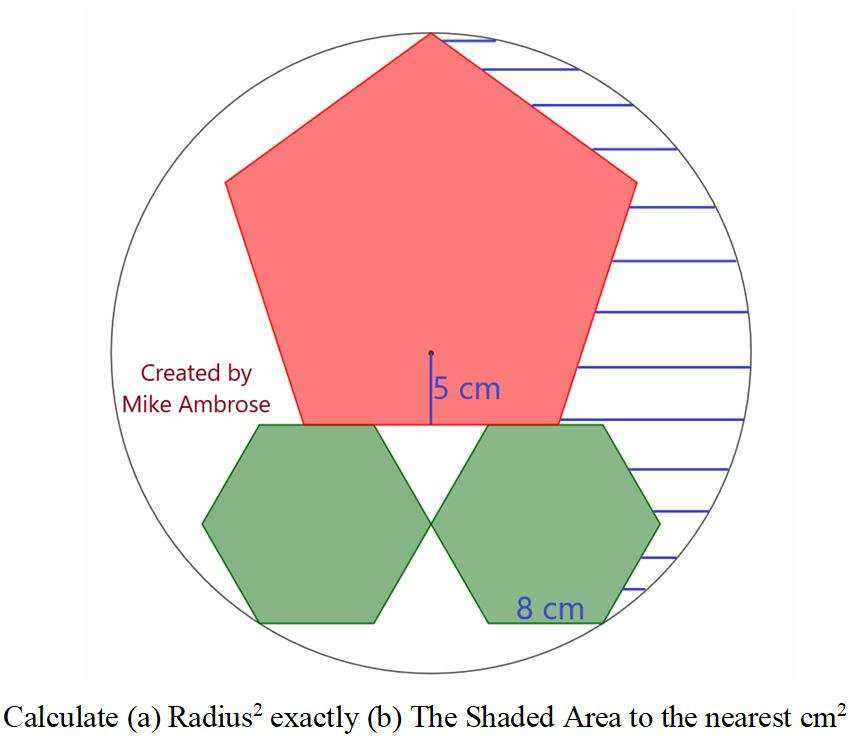
Mathematics Question and Solution
Notice;
Green regular hexagon's side is 8 cm.
sin60 = a/8
a = 4√(3) cm
Where a is the the height of the white triangle enclosed by the two green regular hexagon and the regular pentagon.
b = 2a
b = 8√(3) cm.
c = 5+b
c = (5+8√(3)) cm.
d = 8+4
d = 12 cm.
(a) Calculating Radius² exactly.
Let r be radius.
It implies;
r² = 12²+(5+8√(3))²
r² = (361+80√(3)) cm²
Therefore;
Radius, r of the ascribed circle is;
√(361+80√(3))
r = 22.3509298376 cm.
(b) Calculating area Shaded.
e = atan(12/(5+8√(3)))°
f = 2e
f = 2atan(12/(5+8√(3)))°
f = 64.94441152865°
g = 5+r
g = 27.3509298376 cm.
tan72 = 27.3509298376/
h
h = 8.88685581452 cm.
i = 2h
i = 17.77371162904 cm.
Where i is the side length of the regular pentagon.
Therefore;
Area Shaded to the nearest cm² is;
Area semi-circle with radius 22.3509298376 cm - ½(area regular pentagon with side 17.77371162904 cm) - Area equilateral triangle with side 8 cm - Area regular hexagon with side 8 cm - ½(area sector with radius 22.3509298376 cm and angle 64.94441152865° - area triangle with height 22.3509298376 cm and base 22.3509298376sin(64.94441152865)
½(π*22.3509298376²) - ¼(5*17.77371162904²)*1/(2tan(180/5)) - ½*8²*sin60 - ½(6*8²)*1/(2tan(180/6)) - ½(64.94441152865π*22.3509298376²/360 - ½*22.3509298376²sin64.94441152865)
= 784.71339768076 - 271.75355613693 - 27.7128129211 - 166.27687752661 - 141.56319397507 + 113.13843876327
= 290.54539588432
≈ 291 cm²