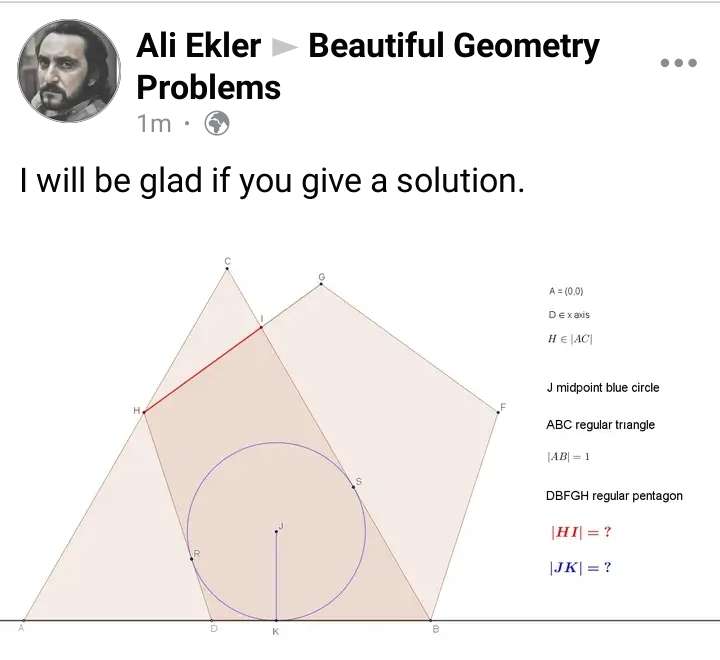
Mathematics Question and Solution
Notice;
Triangle ABC is equilateral.
Let the side of the regular pentagon be a.
Single interior angle of the regular pentagon is;
⅕(180*3)
= 108°
(HF)² = 2a²-2a²cos108
HF = 1.61803398875a units.
sin18 = b/a
b = 0.30901699437a units.
c = HF-b
c = 1.61803398875a-0.30901699437a
c = 1.30901699438a units.
d = 1-c
d = (1-1.30901699438a) units.
cos18 =e/a
e = 0.9510565163a units.
Calculating a, side length of the regular pentagon.
tan60 = e/d
√(3) = 0.9510565163a/(1-1.30901699438a)
√(3)-2.26728394224a = 0.9510565163a
√(3) = 3.21834045854a
a = √(3)/3.21834045854
a = 0.53818134839 units.
AD = 1-0.53818134839
AD = 0.46181865161 units.
(0.46181865161/sinf) = (0.53818134839/sin60)
f = 48°
f is angle AHD.
g = 180-108-48
g = 24°
g is angle CHI.
h = 180-48-60
h = 72°
h is angle ADH.
(0.53818134839/sin60) = (AH/sin72)
AH = 0.59102293778 units.
CH = 1-0.59102293778
CH = 0.40897706222 units.
j = 180-60-24
j = 96°
j is angle CIH.
Therefore;
Length HI is;
(HI/sin60) = (0.40897706222/sin96)
HI = 0.35613547283 units.
Calculating JK, radius of the inscribed circle.
Notice;
Dk + BK = BD.
And BD = a = 0.53818134839 units.
Calculating DK and BK.
Let Jk = r.
tan54 = r/DK
DK = (r/tan54)
DK = 0.72654252801r --- (1).
tan30 = r/Bk
BK = (r/tan30)
BK = 1.73205080757r --- (2).
Therefore;
(1) + (2) = BD
0.72654252801r+1.73205080757r = 0.53818134839
2.45859333558r = 0.53818134839
r = 0.53818134839/2.45859333558
r = 0.21889807501 units.
It implies;
JK = 0.21889807501 units.