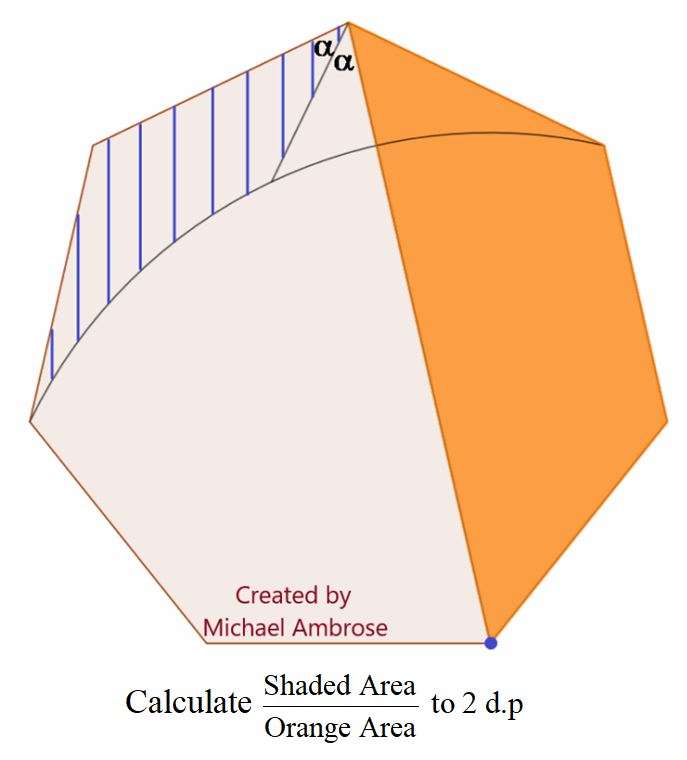
Mathematics Question and Solution
Let the side length of the regular heptagon be 1 unit.
a = ⅐(180*5)
a = ⅐(900)°
b = 0.5(360-2(900/7))
b = ⅐(360)°
c = 2cos(360/7)+1
c = 2.24697960372 units.
d² = 2-2cos(90/7)
d = 1.8019377358 units.
Where d is the radius of the arc.
Area Orange is;
0.5*2.24697960372*1sin(360/7)+0.5*sin(900/7)
= 1.26929543856 square units.
Let e be alpha.
Calculating e.
e = 0.5((900/7)-(360/7))
e = ⅐(270)°
(1.8019377358/sin(270/7)) = (2.24697960372/sinf)
f = 128.96966294132°
g = 180-f-e
g = 12.45890848725°
h = 0.5(180-(900/7))
h = 25.71428571429°
i = (540/7)-g-h
i = (540/7)-12.45890848725-25.71428571429
i = 38.96966294132°
j = ((540/7)-25.71428571429)°
Area Shaded is;
0.5*1.8019377358*2.24697960372sin((540/7)-25.71428571429)+0.5sin(900/7)-0.5*1.8019377358*2.24697960372sin12.45890848725-38.96966294132π*1.8019377358*1.8019377358/360
= 1.58278552297-1.15005455564
= 0.43273096733 square units.
Area Shaded ÷ Area Orange to 2 decimal places is;
0.43273096733÷1.26929543856
= 0.34092217949
≈ 0.34