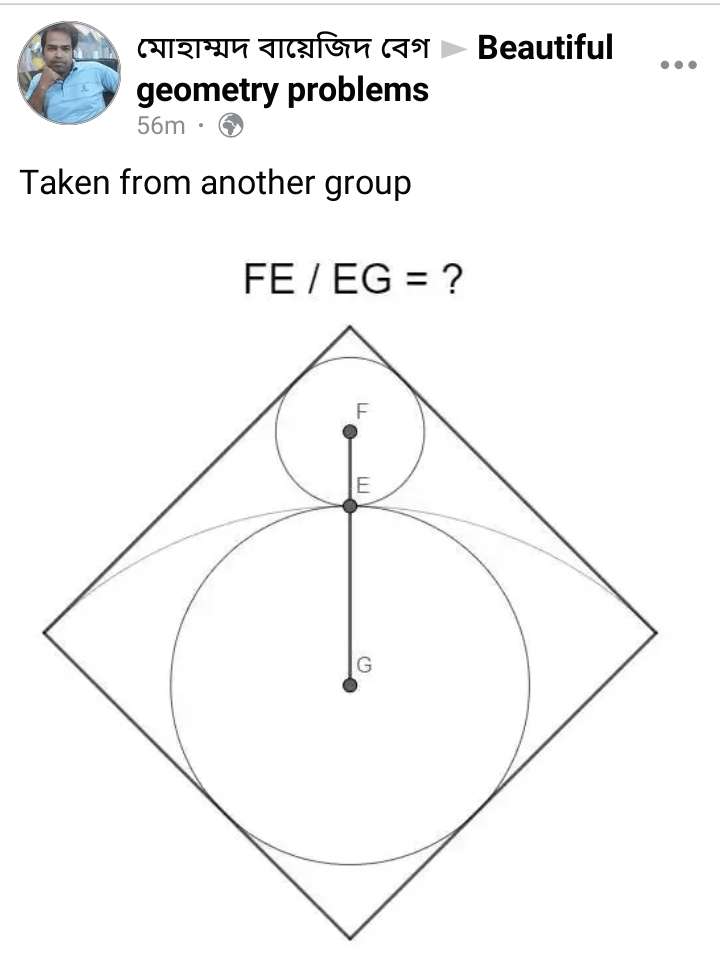
Mathematics Question and Solution
Let the side length of the square be 2 units.
Let the radius of the small inscribed circle be x.
Let the radius of the big inscribed circle be y.
Calculating y.
(2-y)² = y²+y²
2-y = √(2)y
2 = √(2)y+y
It implies;
y = 2/(√(2)+1) units.
y = 0.82842712475 units
Where y is EG.
Calculating x.
(2+x)² = 2(2-x)²
4+4x+x² = 2(4-4x+x²)
4+4x+x² = 8-8x+2x²
x²-12x+4 = 0
Solving the quadratic equation using completing the square approach to get x.
(x-6)² = -4+(-6)²
(x-6)² = 32
x-6 = ±4√(2)
x = 6±4√(2)
Therefore;
x ≠ 6+4√(2) units
x = 6-4√(2) units.
x = 2(3-2√(2)) units.
x = 0.34314575051 units.
Where x is FE.
Therefore;
FE÷EG
= 0.34314575051÷0.82842712475
= 0.41421356237