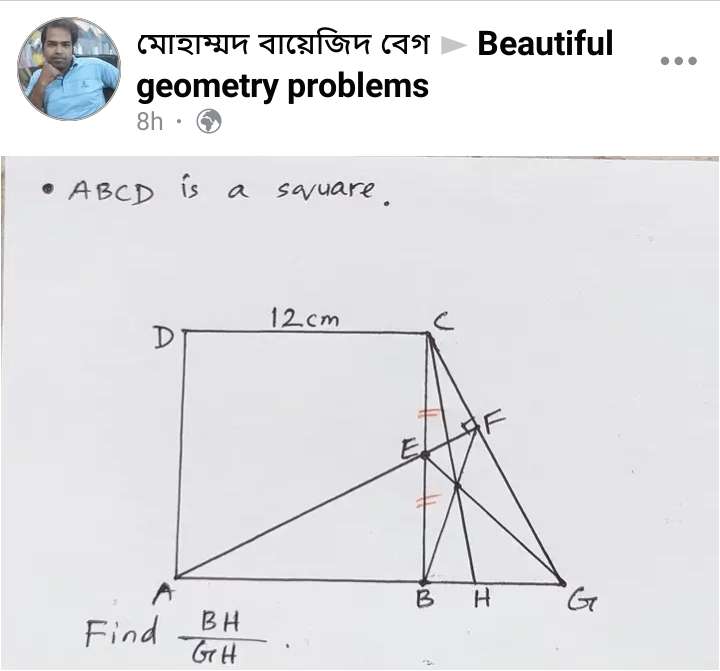
Mathematics Question and Solution
AC = √(12²+12²)
AC = 12√(2) cm.
AE = √(12²+6²)
AE = 6√(5) cm.
Angle BAE = atan(½)°
Angle CAE = 45-atan(1/2)
Angle CAE = 18.43494882292°
cos18.43494882292 = (AF)/12√(2)
AF = 16.099689438 cm.
EF = AF-AE
EF = 16.099689438-6√(5)
EF = 2.683281573 cm.
Angle BCG = 90-45-18.43494882292
Angle BCG = 26.56505117708°
tan26.56505117708 = (BG)/12
BG = 6 cm.
CF = √(6²-2.683281573²)
CF = 5.366563146 cm.
(BF)² = 16.099689438²+12²-24*16.099689438cos(atan(1/2))
BF = 7.58946638441 cm.
(7.58946638441/sin(atan(0.5))) = (16.099689438/sina)
a = 108.43494882293°
Angle CBF = 108.43494882293-90
Angle CBF = 18.43494882293°
Angle FBG = 90-18.43494882293 = 71.56505117707°
(EG)² = 6²+(6√(5))²-72√(5)cos(atan(0.5)
EG = 8.48528137424 cm.
(8.48528137424/sin(atan(0.5))) = (6/sinb)
b = 18.43494882293°
b is angle CGE.
Angle BGE = atan(2)-18.43494882292 = 45°
d = 180-45-71.56505117707
d = 63.43494882293°
(6/sin63.43494882293) = (e/sin45)
e = 4.74341649025 cm.
f² = 4.74341649025²+12²-24*4.74341649025cos18.43494882293
f = 7.64852927039 cm.
(7.64852927039/sin18.43494882293) = (4.74341649025/sing)
g = 11.30993247401°
g is angle BCH.
It implies;
tan11.30993247401 = BH/12
BH = 2.4 cm.
BH = (12/5) cm.
BH = 2⅖ cm.
Therefore;
GH= BG-BH
GH = 6-2⅖
GH = 6-(12/5)
GH = (18/5) cm.
GH = 3⅗ cm.
Therefore;
Length BH ÷ Length GH is;
(12/5)÷(18/5)
= ⅔