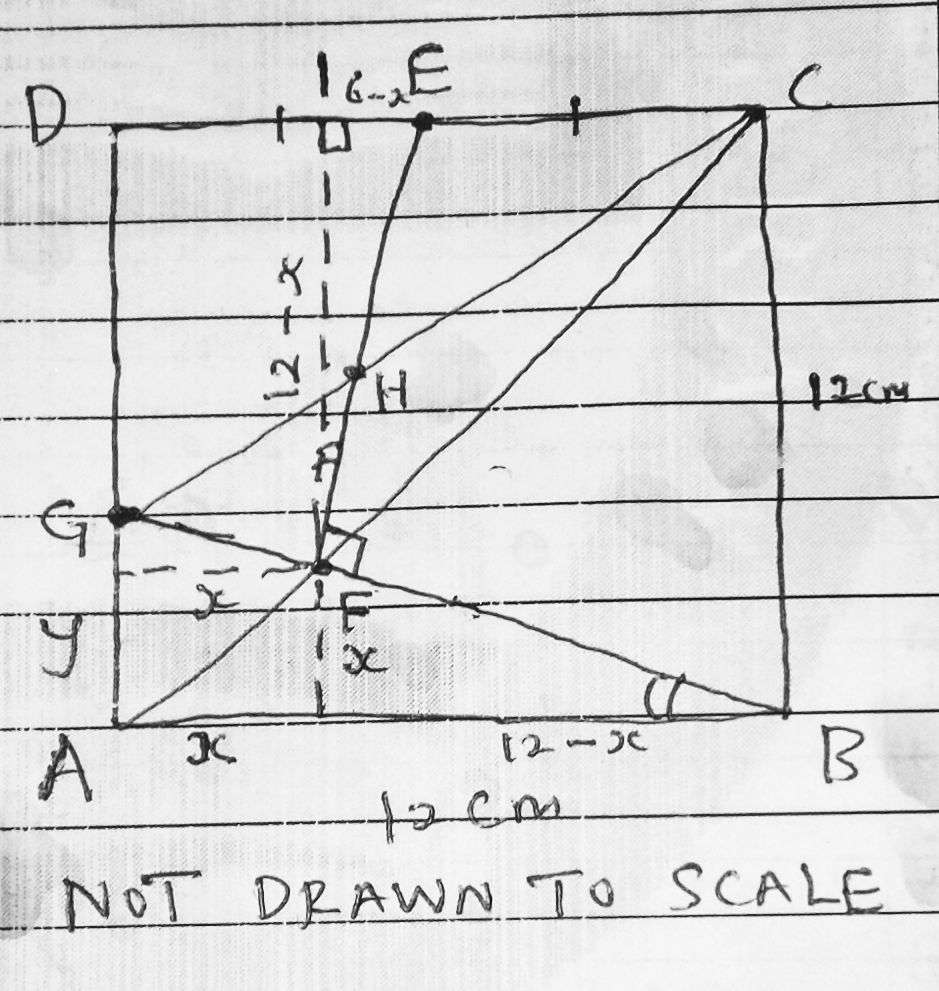
Mathematics Question and Solution
Please, move a step right to review the analyzed figure.
Considering similar triangle ABG ratios.
AG = x
12 = 12-x
It implies;
AG = 12x/(12-x)
Notice;
Angle ABG = Angle EFI, therefore considering similar triangle ratios of the both triangles.
(6-x) = 12x/(12-x)
(12-x) = 12
It implies;
12(6-x) = (12-x)(12x/(12-x))
72-12x = 12x
24x = 72
x = 3 cm.
Therefore;
AG = 4 cm.
DG = 8 cm.
Angle ABG = Angle EFI = atan(⅓)°
(CG)² = 12²+8²
CG = 4√(13) cm.
Angle FEI = atan(3)°
Angle CEH = (180-atan(3))° = 108.43494882292°
Angle DCG = atan(2/3)°
Angle CHE = 180-108.43494882292-atan(2/3) = 37.8749836511°
Calculating CH.
(CH/sin108.43494882292) = (6/sin37.8749836511)
CH = 9.27141756548 cm.
Calculating GH.
GH = CG-CH
GH = 4√(13)-9.27141756548
GH = 5.15078753638 cm.
(EF)² = 9²+3²
EF = 3√(10) cm.
Calculating EH.
(EH/sin(atan(2/3)) = (6/sin37.8749836511)
EH = 5.42104741743 cm.
Calculating FH
FH = EF-EH
FH = 3√(10)-5.42104741743
FH = 4.06578556307 cm.
Therefore;
1. CH ÷ GH
= 9.27141756548÷5.15078753638
= 1.8
= 9/5
2. EH ÷ FH
= 5.42104741743÷4.06578556307
= 1.33333333333
= 4/3