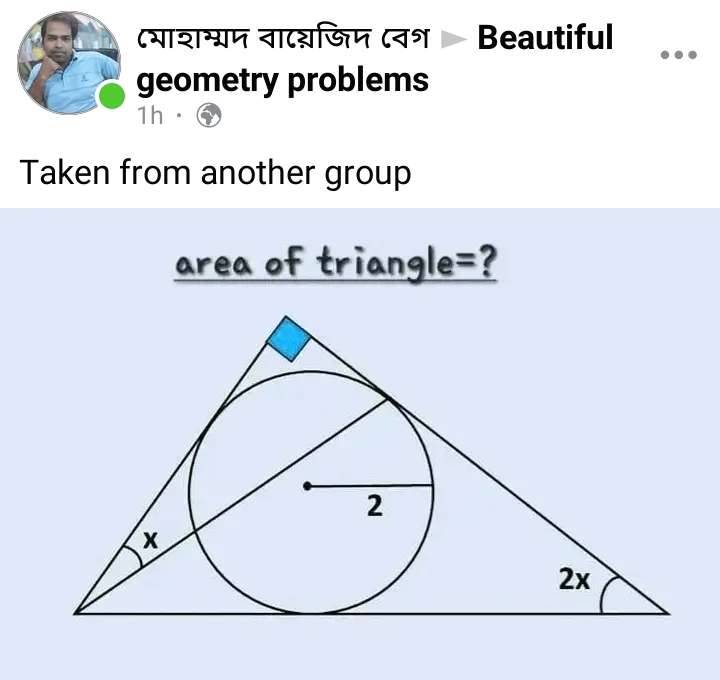
Mathematics Question and Solution
tanx = 2/a
a = 2/tanx ----- (1).
b = a+2
b = (2/tanx) + 2 ----- (2).
Notice;
a = the short adjacent length of the right-angled triangle.
b = the long adjacent length of the right-angled triangle.
Let tanx = c.
Calculating the hypotenuse of the right-angled triangle.
(2/c)-2+(2/c)
= (4/c)-2
= (4-2c)/c units.
It implies;
Using sum of areas derived that are inscribed the ascribed triangle to equal the area of the ascribed triangle to find c.
2(2/c)+2(2c+2)/c+2(4-2c)/c = (2/c)((2c+2)/c)
(4+4c+4+8-4c)/c = (4c+4)/c²
16 = (4c+4)/c
16c = 4c+4
12c = 4
c = ⅓
And
tanx = c
tanx = ⅓
x = atan(⅓)°
It implies;
a = 2/tanx, and x = atan(⅓)
a = 2/tan(atan(⅓))
a = 2/(⅓)
a = 6 units.
b = a+2, and a = 6 units.
b = 6+2
b = 8 units.
Notice;
a and b is the adjacent base and adjacent height of the right-angled triangle respectively.
Therefore;
Area of the ascribed right-angled triangle is;
½(ab)
= ½(6*8)
= 24 square units.