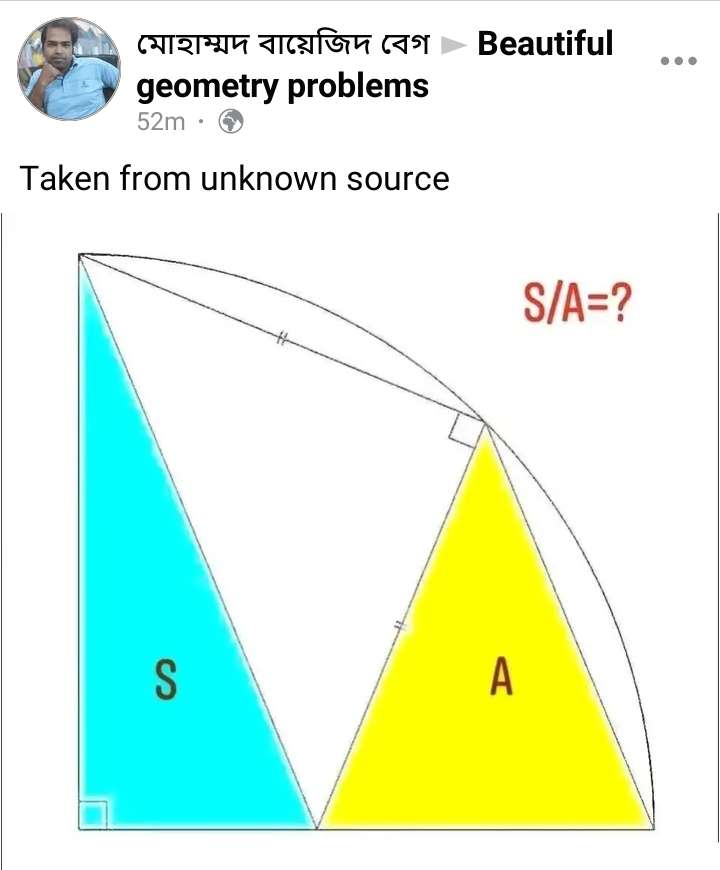
Mathematics Question and Solution
Let the ascribed quarter circle be 2 units.
2a² = 2²
a² = 2
a = √(2) units.
b = (2-√(2)) units.
c² = (√(2))²+(2-√(2))²
c² = 2+4-4√(2)+2
c² = 8-4√(2)
c = √(8-4√(2)) units.
d² = √(8-4√(2))²-√(2)²
d² = 8-4√(2)-2
d² = 6-4√(2)
d = √(6-4√(2)) units.
tane = √(2)/(√(6-4√(2)))
e = atan(√(2)/(√(6-4√(2))))
e = 67.5°
f = 180-45-67.5
f = 67.5°
tan67.5 = 2/g
g = 0.82842712475 units.
h = 2-0.82842712475
h = 1.17157287525 units.
Therefore;
Area Triangle S is;
0.5*2*0.82842712475
= 0.82842712475 square units.
Area Triangle A is;
0.5*1.17157287525* 1.53073372946sin67.5
= 0.82842712474 square units.
It implies;
Area Triangle S ÷ Area Triangle A is;
0.82842712475÷0.82842712474
= 1