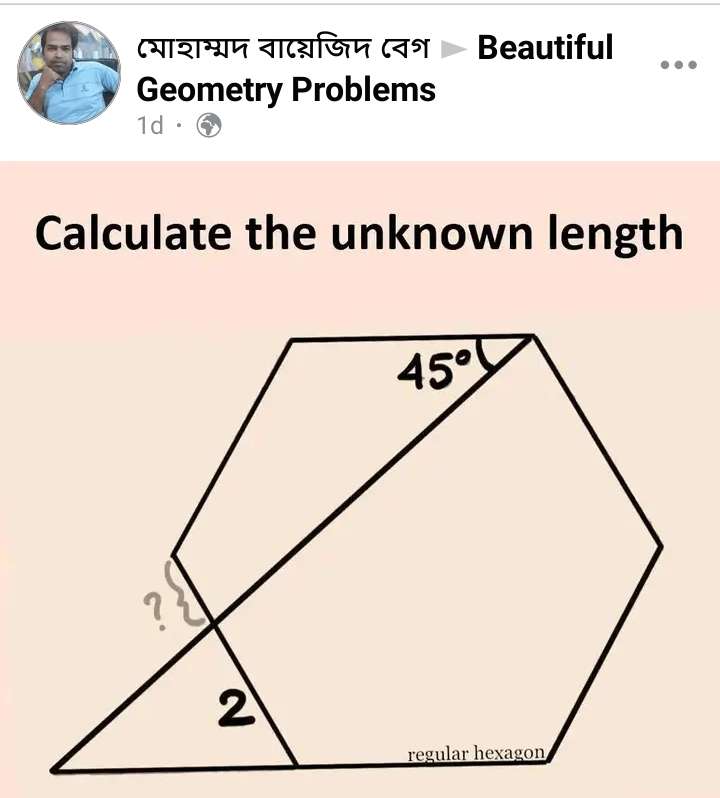
Mathematics Question and Solution
Let the side of the regular hexagon be a.
Calculating a
b = 180-60-45
b = 75°
(c/sin75) = (2/sin45)
c = (1+√(3)) units.
d² = 2a²-2a²cos120
d = √(3a²)
d = √(3)a ----- (1).
e = c+a, and c = (1+√(3)) units.
e = (1+√(3)+a) --- (2).
Therefore equating (1) and (2).
√(3)a = 1+√(3)+a
√(3)a-a = √(3)+1
a(√(3)-1) = √(3)+1
a = (√(3+1)/(√(3)-1)
a = (√(3)+2) units.
It implies;
The required length is;
a-2
Where a is the side length of the regular hexagon, (√(3)+2) units.
= √(3)+2-2
= √(3) units.