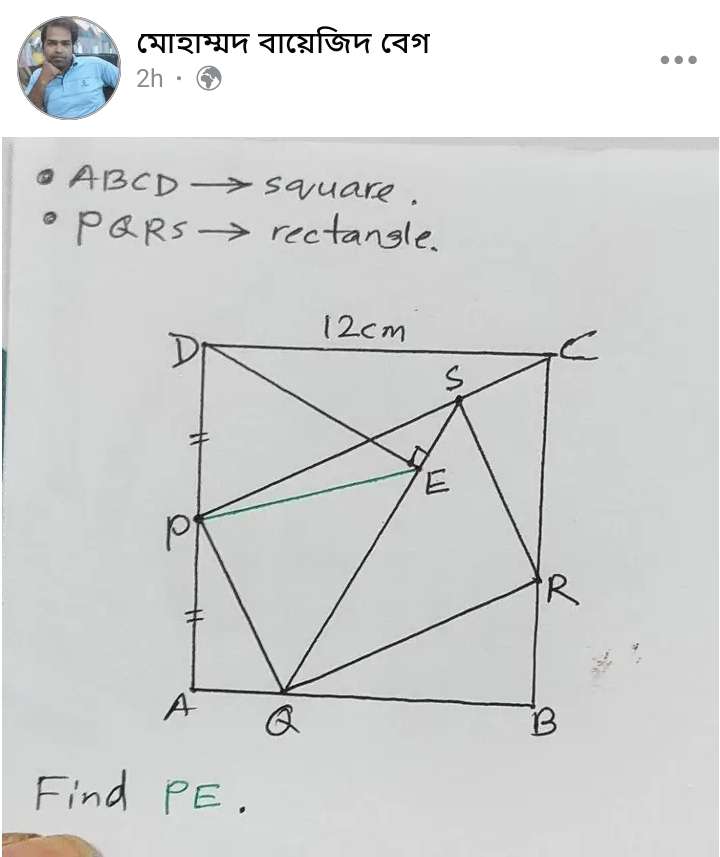
Mathematics Question and Solution
Calculating AQ using similar plane shapes (triangle) rule.
12 = 6
6 = a cross multiply.
12a = 36
a = 3 cm.
Where a is AQ.
PQ = √(6²+3²)
PQ =√(45)
PQ = 3√(5) cm.
BQ = 12-3
BQ = 9 cm.
Calculating BR using similar plane shapes (triangle) rule.
6 = 9
3 = b cross multiply.
6b = 27
b = ½(9) cm.
b = 4.5 cm.
Where b is BR.
QR = √(9²+4.5²)
QR = ½(9√(5)) cm.
Calculating angle PQS.
tanc = PS/PQ
c = atan((4.5√(5))÷(3√(5)))
c = atan(3/2)°
Where c is angle PQS.
Angle AQP = atan(2)°
Angle AQD = atan(4)°
Angle ADQ = atan(1/4)°
DQ= √(12²+3²)
DQ = √(153)
DQ = 3√(17) cm.
Angle DQE is;
angle PQS+Angle AQP-Angle ADQ
= atan(3/2)+atan(2)-atan(4)
= 43.78112476487°
It implies;
Angle EDQ is;
90-43.78112476487
= 46.21887523513°
cos46.21887523513 = DE/(3√(17))
DE = 3√(17)cos46.21887523513
DE = 8.55839668666 cm.
Angle EDP is;
46.21887523513°+atan(1/4)°
= 60.25511870306°
It implies;
Green Length PE is;
Let it be d.
d² = 6²+8.55839668666²-2*6*8.55839668666cos60.25511870306
d² = 58.29230769236
d = √(58.29230769236)
d = 7.63493992723 cm.
Therefore Green Length PE is;
= 7.63493992723 cm.