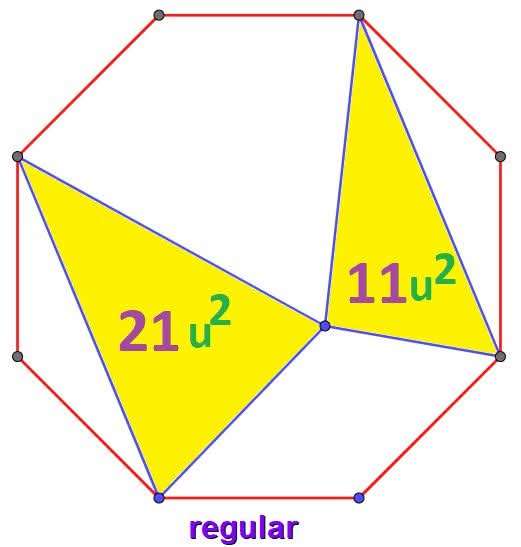
Mathematics Question and Solution
Calculating the area of the ascribed regular octagon.
Let the equal longest length of the both inscribed yellow triangles be x.
a = ⅛*180(8-2))
a = ⅛(180*6)
a = ½(45*6)
a = 135°
a is the single interior angle of the ascribed regular octagon.
sin(0.5*135) = (0.5x)/b
b = 0.54119610015x units.
b is the side length of the regular octagon.
c = 135-(0.5*45)-½(360-2(135))
c = 135-22.5-45
c = 135-67.5
c = 67.5°
c is the second bigger interior angle of inscribed triangle 21 square units.
2e² = (0.54119610015x)²
e = 0.38268343237x units.
f = 2e+b
f = 1.30656296489x unit.
tang = 0.38268343237x/(0.5*0.54119610015x)
g = 54.7356103174°
sin54.7356103174 = 0.38268343237x/h
h = 0.46868957116x units.
j = ½(f)
j = ½(1.30656296489x)
j = 0.65328148245x units.
k = 135-22.5-54.7356103174
k = 57.7643896826°
It implies;
Calculating x.
(0.5*x*0.65328148245xsin67.5)+(0.5*x*0.46868957116xsin57.7643896826) = 21+11
0.3017766953x²+0.1982233047x² = 32
0.5x² = 32
x² = 64
x = 8 units.
Again, x is the equal longest side length of the both inscribed yellow triangles.
Recall.
b = 0.54119610015x units.
And x = 8 units.
b = 0.54119610015*8
b = 4.3295688012 units.
Again, b is the side length of the regular octagon.
Recall.
f = 1.30656296489x unit.
And x = 8 units.
f = 1.30656296489*8
f = 10.4525037191 units.
f is the height of the regular octagon.
Recall Again.
e = 0.38268343237x
And x = 8 units.
e = 0.38268343237*8
e = 3.06146745896 units.
Therefore, Area Ascribed Regular Octagon is;
(b*f)+2(½(b+f)e)
= (4.3295688012*10.4525037191)+2(½(4.3295688012+10.4525037191)*3.06146745896
= 45.2548339966+(14.7820725203*3.06146745896)
= 45.2548339966+45.2548339969
= 90.5096679935 square units.