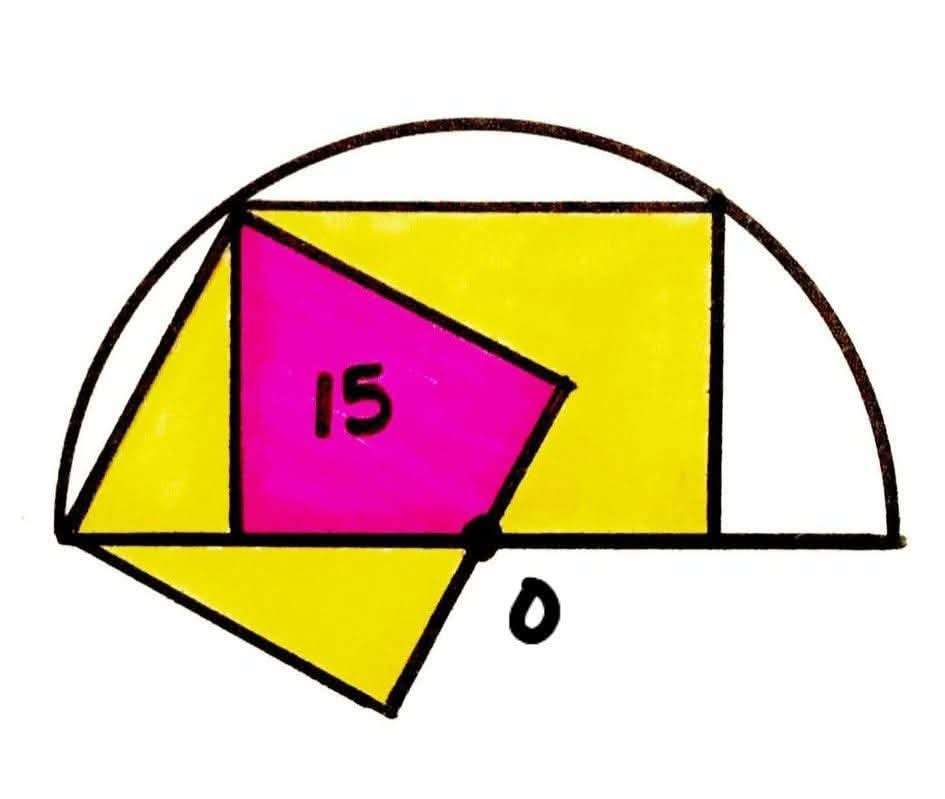
Mathematics Question and Solution
Calculating Yellow Area.
Let a be the side length of the square.
b = ½(a) units.
c² = a²+(½(a))²
c² = ¼(5a²)
c = ½√(5)a units.
c is the radius of the half circle.
It implies;
a ~ ½√(5)a
d ~ a
Cross Multiply.
½√(5)d = a
d = 2a/√(5)
d = ⅕(2√(5)a) units.
e = ½(d)
e = ⅕√(5)a units.
f = c-e
f = ½√(5)a-⅕√(5)a
f = ⅒(3√(5))a units.
Calculating a.
½*a*½(a)+½*⅒(3√(5))a*⅕(2√(5)a) = 15
¼(a²)+⅒(3a²) = 15
5a²+6a² = 300
11a² = 300
a = 10√(3)/√(11)
a = 10√(33)/11 units.
g = 2f
g = 2*⅒(3√(5))a
g = ⅕(3√(5))a units
a² = (10√(33)/11)²
= (100*33)/(11*11)
= 300/11 square units.
a² is the area of the square.
h = d*g
h = ⅕(2√(5)a)*⅕(3√(5))a
h = ⅕(6a²)
And a² = 300/11 square units.
h = ⅕*6*(300/11)
h = (360/11) square units.
h is the area of the inscribed rectangle.
Area yellow is;
a²-15+h-15
= ((300/11)-15)+((360/11)-15)
= (660/11)-30
= 60-30
= 30 square units.