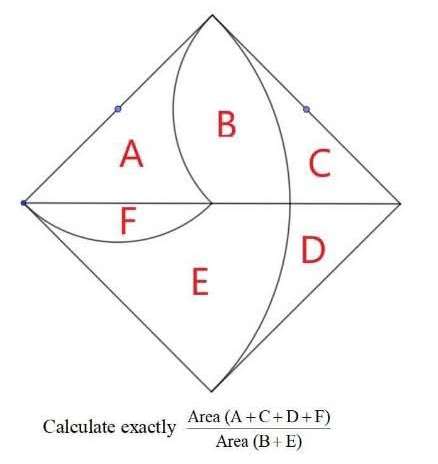
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the square side length be 2 units.
Calculating Area C and D.
Notice.
Area C = Area D.
C = ½(2²-¼(2*2π))
C = ½(4-π) square units.
Therefore;
D = ½(4-π) square units.
Calculating Area F.
F = ¼(1²*π)-½(1*1)
F = ¼(π)-½
F = ¼(π-2) square units.
Calculating Area E.
E = ½(¼*2*2π)-F
E = ½(π)-¼(π-2)
E = ½(π)-¼(π)+½
E = ¼(π)+½
E = ¼(π+2) square units.
Calculating Area A.
A = ½*½(2*2)-F
A = 1-¼(π-2)
A = ½(3)-¼(π)
A = ¼(6-π) square units.
Calculating Area B.
B = ½(¼*2*2π-½*2*2)+F
B = ½(π-2)+¼(π-2)
B = ½(π)-1+¼(π)-½
B = ¼(3π)-½(3)
B = ¼(3π-6) square units.
It implies;
Area (A+C+D+F) ÷ Area (B+E) is;
(¼(6-π)+½(4-π)+½(4-π)+¼(π-2))÷(¼(3π-6)+¼(π+2))
= (5-π)÷(π-1)
= ((5-π)(π+1))÷((π-1)(π+1))
= (5π+5-π²-π)÷(π²-1)
= (5+4π-π²)/(π²-1) Exactly in fraction.
= 0.8677688277 in decimal.