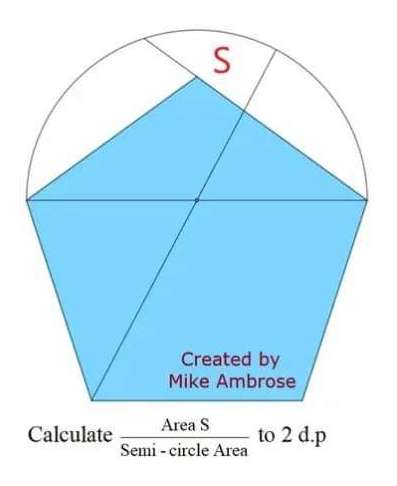
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the side of the regular pentagon be 2 units.
cos36 = a/2
a = 1.61803398875 units.
Where a is the radius of the semi circle.
Area semi-circle is;
½(1.61803398875)²π
= 4.11239817295 square units.
Calculating area S.
b = 108-36
b = 72°
c = 1.61803398875-1
c = 0.61803398875 units.
tan72 = d/0.61803398875
d = 1.90211303259 units.
e = atan(1.90211303259)°
e = 62.26769855229°
(f/sin62.26769855229) = (1.61803398875/sin(180-36-62.26769855229)
f = 1.4472135955 units.
Area S is;
(108π*1.61803398875²/360) - (0.5*1.61803398875²sin108) - (62.26769855229π*1.61803398875²/360) + (0.5*1.4472135955*1.61803398875sin36)
= 2.46743890377 - 1.24494914244 - 1.42260872089 + 0.68819096024
= 0.48807200068 square units.
It implies;
Area S ÷ Area Semi-Circle to 2 decimal places is;
0.48807200068 ÷ 4.11239817295
= 0.11868306038
≈ 0.12