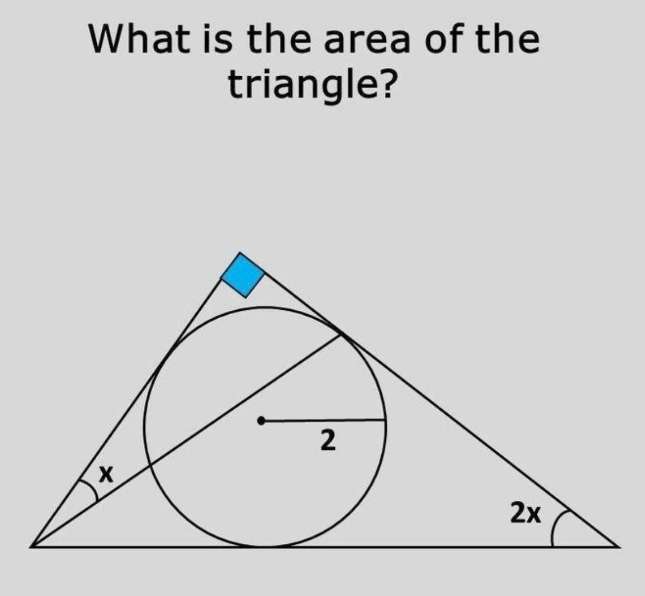
Mathematics Question and Solution
Calculating the area of the ascribed right-angled triangle.
a = (y+2) units.
a is the adjacent base of the right-angled triangle.
b = (z+2) units.
b is the adjacent height of the right-angled triangle.
2 units is the radius of the inscribed circle.
c = (y+z) units.
c is the hypotenuse of the right-angled triangle.
a²+b² = c²
(y+2)²+(z+2)² = (y+z)² --- (1).
tanx = 2/z --- (2).
tanx = 2/(y+2) --- (3).
Equating (2) and (3).
2/z =2/(y+2)
z = y+2 --- (4).
Substituting (4) in (1).
(y+2)²+(y+2+2)² = (y+y+2)²
(y+2)²+(y+4)² = (2y+2)²
y²+4y+4+y²+8y+16 = 4y²+8y+4
2y²+12y+20 = 4y²+8y+4
2y²-4y-16 = 0
y²-2y = 8
(y-1)² = 8+(-1)²
y-1 = ±√(9)
y = 1±3
It implies;
y ≠ 1-3 = -2
y = 1+3 = 4 units.
Recall.
a = (y+2) units.
And y = 4 units.
a = 4+2
a = 6 units.
Again, a is the adjacent base of the right-angled triangle.
Recall again.
z = y+2 at (4).
And y = 4 units.
z = 4+2
z = 6 units.
Recall again please.
b = (z+2) units.
And z = 6 units.
b = 6+2
b = 8 units.
Again, b is the adjacent height of the right-angled triangle.
Therefore;
Area triangle, right-angled triangle is;
½*ab
= ½*6*8
= ½(48)
= 24 square units.