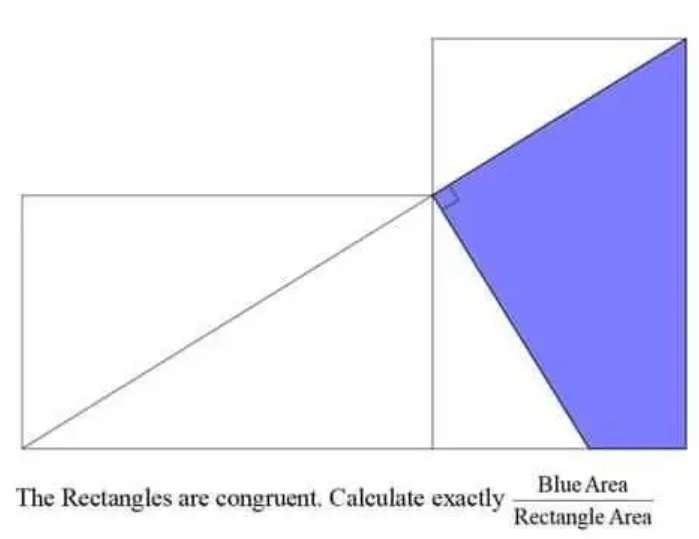
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the length of the two congruent rectangles be x.
Let their width be y.
Therefore area rectangle is;
x * y
= xy square units.
Area blue is;
Area rectangle with length x units and width y units unit - 2(area triangle with height y units and base (y²/x) units).
= xy - 2*½(y³/x)
= (x²y-y³)/x square units.
Area blue ÷ Area rectangle is;
(x²y-y³)/x ÷ xy
= (x²y-y³)/x²y
= 1 - (y/x)²
Notice;
Considering two similar triangles.
The first with base x unit and height y units.
The second with base (x+y) units and height x unit.
Therefore;
y ~ x
x ~ (x+y)
Cross Multiply.
y/x = x/(x+y)
xy+y²=x²
Divide through by xy.
1+(y/x)=(x/y)
Let (x/y) = a
Therefore;
1+(1/a)=a
a+1=a²
a²-a-1=0
(a-½(a))²= 1+¼
a = ½±½√(5)
a > 0
a = ½(1+√(5))
And (x/y) = a = ½(1+√(5))
Therefore;
(y/x) = 1/a = 2/(1+√(5))
Substituting (y/x) in 1 - (y/x)²
= 1 - (2/(1+√(5)))²
= 1 - (2-2√(5)/(-4))²
= 1 - ((4-8√(5)+20)/(16))
= 1 -- ((24-8√(5))/16)
= (16-24+8√(5))/16
= (8√(5)-8)/16
= 8(√(5)-1)/16
= ½(√(5)-1)