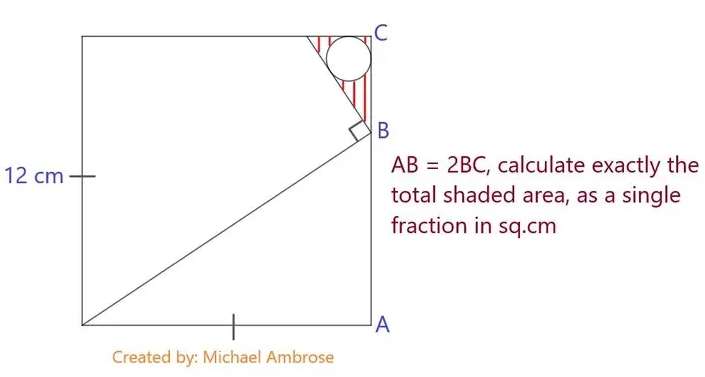
Mathematics Question and Solution
Since;
AB = 2BC
It implies;
AB = (2/3)*12
AB = 8 cm.
BC = (1/3)*12
BC = 4 cm.
12 cm is the side length of the ascribed square.
tana = 12/8
a = atan(3/2)°
b = 90-a
b = atan(2/3)°
2/3 = c/4
c = (8/3) cm.
d² = 4²+(8/3)²
d = ⅓(4√(13)) cm.
Calculating e, radius of the inscribed circle.
(8/3)e+4e+(4√(13)/3)e = (8/3)*4
⅓(20+4√(13))e = (32/3)
e = 32/(20+4√(13))
e = 0.929632483 cm.
Again, e is the radius of the inscribed circle.
Therefore, shaded area exactly in decimal is;
(½*(8/3)*4)-(π0.929632483²)
= 2.6183169578 cm²