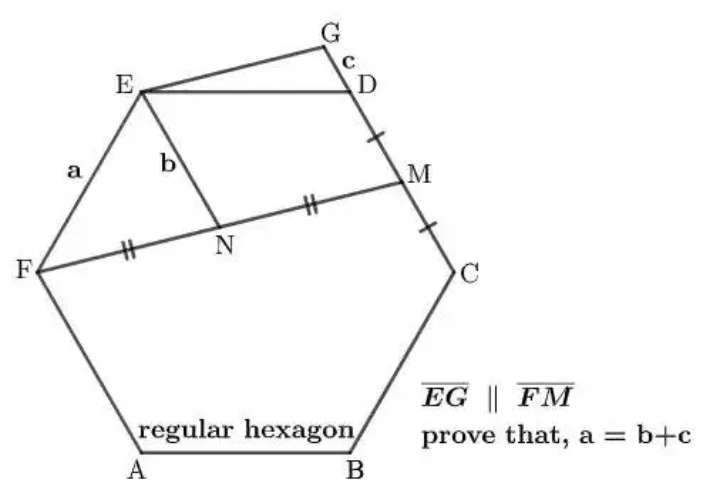
Mathematics Question and Solution
Let a be 1 unit.
d = ⅙*180(6-2)
d = 120°
d is the single interior angle of the regular hexagon.
cos60 = e/1
e = 0.5 units.
f = a+2e
f = 2 units.
f is CF.
g² = 0.5²+2²-2*0.5*2cos60
g = 1.8027756377 units.
g is MF.
(1.8027756377/sin60) = (0.5/sinh)
h = 13.897886248°
h is angle CFM.
j = 60-h
j = 46.102113752°
j is angle EFN.
k = ½(g)
k = 0.9013878189 units.
k is FN = MN.
Calculating b.
b² = 0.9013878189²+1²-2*0.9013878189*1cos46.102113752
b = 0.75 units.
b is EN.
Notice.
EN = GM = b = 0.75 units.
Calculating c (DG).
c+ DM = b
And b = 0.75 unit
while DM = ½(a) = 0.5 units.
It implies;
c = b-DM
c = 0.75-0.5
c = 0.25 units.
It implies;
a = 1 unit, b = 0.75 units and c = 0.25 units.
Therefore;
a = b+c
Proved.