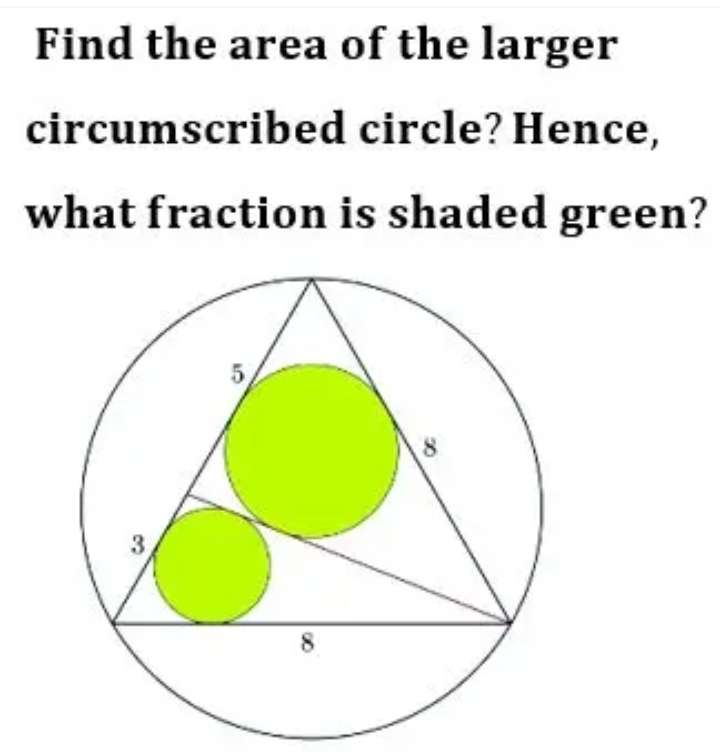
Mathematics Question and Solution
Let a be the radius of the larger circumscribed circle.
Calculating a.
cos30 = 4/r
½√(3) = 4/r
r = 8/√(3)
r = ⅓(8√(3)) units.
Therefore, area circumscribed circle is;
π(8/√(3))²
= ⅓(64π) square units.
Calculating the area of the two inscribed green circles.
b² = 3²+8²-2*3*8cos60
b² = 73-24
b = √(49) units.
b = 7 units.
Let c be the radius of the big inscribed green circle.
Calculating c.
3c+7c+8c = 3*8sin60
18c = 12√(3)
c = ⅓(2√(3)) units.
Area big inscribed green circle is;
πc²
= π(⅓(2√(3)))²
= ⅓(4π) square units.
Let d be the radius of the bigger inscribed green circle.
Calculating d.
5d+7d+8d = 5*8sin60
20d = 20√(3)
d = √(3) units.
Area bigger inscribed green circle is;
πd²
= π√(3)²
= 3π square units.
Therefore, area green total is;
⅓(4π)+3π
= ⅓(13π) square units.
Hence, the fraction shaded green is;
Area green total ÷ Area circumscribed larger circle.
= ⅓(13π) ÷ ⅓(64π)
= 13/64