Mathematics Question and Solution
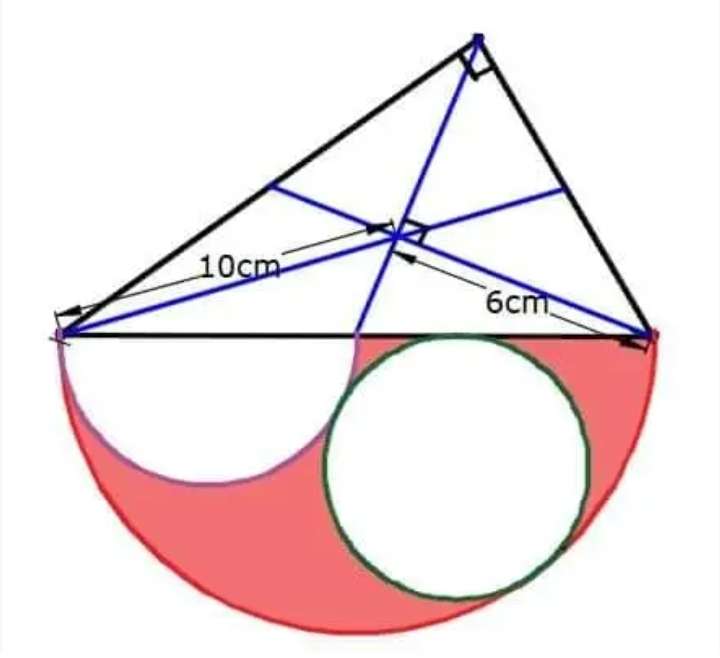
Calculating shaded red area.
Let a be the diameter of the inscribed big half circle.
Therefore, 2a is the diameter of the bigger half circle or a is the radius of the bigger half circle.
a² = 6²+b²
b = √(a²-36) cm.
6 - c
a - √(a²-36)
Cross Multiply.
c = (6√(a²-36))/a cm.
Again.
a - √(a²-36)
√(a²-36) - d
Cross Multiply.
d = (a²-36)/a cm.
e = a+d
e = (2a²-36)/a cm.
Calculating a.
10² = ((2a²-36)/a)²+((6√(a²-36))/a)²
100 = ((4a⁴-144a²+1296)/a²)+((36a²-1296)/a²)
100a² = 4a⁴-108a²
4a⁴ = 208a²
4a² = 208
a² = 52
a = √(52)
a = 2√(13) cm.
a = 7.2111025509 cm.
Again, a is the radius of the bigger half circle or the diameter of the big inscribed half circle.
f = ½(a)
f = √(13) cm.
f is the radius of the inscribed big half circle.
Let g be the radius of the inscribed circle.
h = (2√(13)-g) cm.
j²+g² = (2√(13)-g)²
j² = 52-4√(13)g+g²-g²
j = √(52-4√(13)g) cm.
k = f+j
k = (√(13)+√(52-4√(13)g)) cm.
l = (√(13)+g) cm.
Calculating g.
(√(13)+g)² = (√(13)+√(52-4√(13)g))²+g²
13+2√(13)g+g² = 13+2√(13)*√(52-4√(13)g)+52-4√(13)g+g²
2√(13)g = 2√(13)*√(52-4√(13)g)+52-4√(13)g
2√(13)g = 2√(13(52-4√(13)g)+52-4√(13)g
√(13)g = √(13(52-4√(13)g)+26-2√(13)g
3√(13)g-26 = √(13(52-4√(13)g)
(3√(13)g-26)² = 13(52-4√(13)g)
117g²-156√(13)g+676 = 676-52√(3)g
117g² = 156√(13)g-52√(3)g
117g² = 104√(13)g
9g = 8√(13)
g = ⅑(8√(13)) cm.
g = 3.2049344671 cm.
Again, g is the radius of the inscribed circle.
Therefore, shaded red area is;
Half area circle with radius 2√(13) cm - Half area circle with radius √(13) cm - Area circle with radius ⅑(8√(13)) cm.
= ½*π(2√(13))²-½*π(√(13))²-π(⅑(8√(13)))²
= 26π-½(13π)-(832π/81)
= (4212π-1053π-1664π)/162
= 1495π/162 cm²
= 28.9918581304 cm²
≈ 29 cm²