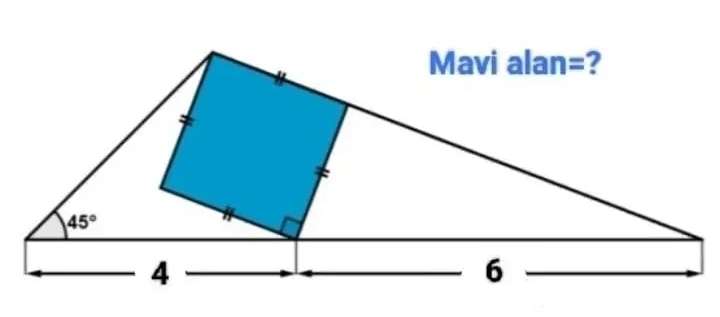
Mathematics Question and Solution
Let the side length of the inscribed blue square be a.
b²+a² = 6²
b = √(36-a²) units.
c = a+b
c = (a+√(36-a²)) units.
It implies;
(a+√(36-a²)) - 6
10 - (a+√(36-a²))
Cross Multiply.
60 = (a+√(36-a²))²
√(60) = a+√(36-a²)
(2√(15)-a)² = 36-a²
60-4√(15)a+a² = 36-a²
2a²-4√(15)a+24 = 0
a²-2√(15)+12 = 0
(a-√(15))² = -12+√(15)²
a = √(15)±√(3)
It implies;
a = √(15)-√(3)
a = √(3)(√(5)-1) units.
a = 2.1409325386 units.
Again, a is the side length of the inscribed blue square.
Therefore, area inscribed blue square is;
a²
= (√(15)-√(3))²
= 3(√(5)-1)²
= 3(5-2√(5)+1)
= 3(6-2√(5))
= 6(3-√(5)) square units.
= 4.583592135 square units.