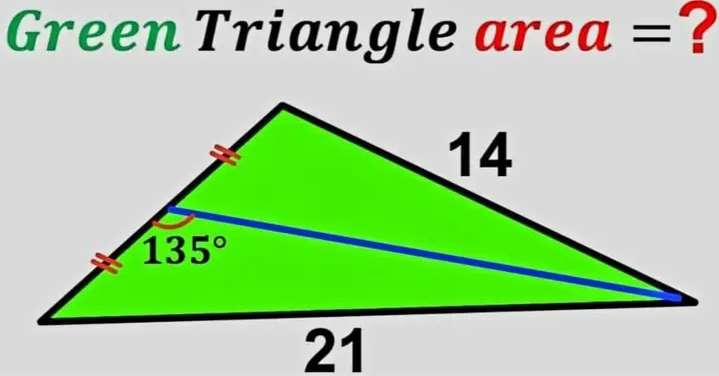
Mathematics Question and Solution
Let the two congruent lengths be a each.
21² = a²+b²+2abcos135
441 = a²+b²+√(2)ab --- (1)
14² = a²+b²-2abcos45
196 = a²+b²-√(2)ab --- (2)
Adding (1) to (2).
637 = 2a²+2b²
b² = ½(637-2a²) --- (3).
b = √(½(637-2a²)) --- (4).
Substituting (3) and (4) in (1) to get a.
441 = a²+½(637-2a²)+√(2)a√(½(637-2a²))
441 = a²+½(637-2a²)+a√(637-2a²)
882 = 2a²+637-2a²+2a√(637-2a²)
245 = 2a√(637-2a²)
245² = 4a²(637-2a²)
60025 = 2548a²-8a⁴
8a⁴-2548a²+60025 = 0
It implies;
a = 5.06145 units.
b = √(½(637-2a²))
And a = 5.06145 units.
b = √(0.5(637-2*5.06145))
b = 17.113787538 units.
Therefore, area triangle green is;
(0.5*5.06145*17.113787538sin45)+(0.5*5.06145*17.113787538sin135)
= 2(0.5*5.06145*17.113787538sin45)
= (5.06145*17.113787538sin45)
= 61.25 square units.